Hash-Based Signature Schemes for Post-Quantum Bitcoin

cryptography

In my personal opinion, the most dangerous and unpredictable challenge facing Bitcoin is not political pressure, practical usability, scaling, or economic incentive… It is the threat of quantum computers.

Large and powerful organizations - both political and corporate - have been pouring billions of dollars into developing quantum computers for decades. Ever since Peter Shor published his (in)famous namesake algorithm in 1994, cryptographers have been preparing for “Q-Day” - the day a large, practically usable quantum computer becomes available.

If you’re reading my blog, I can assume you are at least roughly familiar with elliptic curve public/private keys. I’ll simply tell you that a quantum computer of sufficient power would be able to flip an EC public key backwards into its private key - a feat thought to be implausible with ordinary classical computers. You can see how this might be a problem. If you’d like to learn how this can be done in detail, check out Shor’s original paper.

This article won’t dissect the mechanics of how quantum computers break Bitcoin public keys, nor is it intended as a doom-and-gloom FUD-piece about how we should all be digging graves, stocking bunkers, and prepping for day zero of the post-quantum meltdown. I won’t bother to conjecture how long it will take for a powerful quantum computer to be invented - Estimates of when this will occur vary widely even between professional analysts. I will simply assume it will happen, one day, eventually. When it does, we must deal with it.

My hope is that this article will show you the landscape of the quantum threats facing the Bitcoin community. Then I’ll explore various hash-based signature schemes and analyze their potential to diffuse these threats, and the tradeoffs which inevitably come with them. Finally, I’ll propose a novel upgrade path for Bitcoin clients which uses hash-based cryptography as a fallback option to insure bitcoin users against future quantum adversaries, without the need for any near-term consensus changes.

All safe roads once were wild.

The Quantum Threat

In this section I’ll dive into the mechanics of how exactly a selfish quantum adversary could attack Bitcoin for financial gain. Understanding the fundamental threat of quantum computers in more detail will lead us to clues as to how we can improve our defenses.

Almost every Bitcoin transaction mined from the genesis block to today has authenticated itself using one or more asymmetric signatures. Sometimes public keys are hashed. Sometimes we use Bitcoin script opcodes to encumber coins with additional validation steps (e.g. time delays). But eventually, to spend a Bitcoin UTXO safely, one must be required to supply an asymmetric signature matching some public key committed to by the UTXO itself. The signature must commit to the spending transaction in some way so that it can’t be applied to a different transaction.

If one were to encumber a transaction output with only a hashlock, or only a timelock, etc, with no asymmetric signature requirement, then that UTXO can be spent by anyone who observes it being spent (including the miners who must see the transaction to validate it).

1
OP_SHA256 <hash> OP_EQUAL

A simple hash-lock Bitcoin script pubkey. This script is unspendable until someone reveals the preimage of <hash>. After that, the script could be easily unlocked by anyone.

Bitcoin transactions use signatures on the secp256k1 elliptic curve to achieve this asymmetric authentication dynamic. ECDSA is the older and more well-known signing algorithm, and Schnorr is a cleaner, faster, more secure and more flexible signing algorithm which was adopted several years ago as part of Bitcoin’s Taproot upgrade. Bitcoin’s Schnorr and ECDSA signing protocols both use the same secp256k1 elliptic curve.

ECDSA and Schnorr signing protocols are equally vulnerable to a quantum adversary (QA) who knows a victim’s secp256k1 public key, because the QA can simply invert the public key into the private key, and sign any message they desire.

However, the same QA will have a much harder time computing the preimage (i.e. input) of a hash function given its output. The currently-known best-case-scenario for a QA brute-forcing a hash preimage is a quadratic speed boost, given by Grover’s algorithm. Quadratic in this context means that if a classical computer requires operations to do something, then the QA can do it in operations. The smallest hash used in Bitcoin output scripts is RMD160 which has a security level of , so a quantum computer could crack a preimage to RMD160 in at most operations. Not great, but still implausibly difficult according to current theory.

So not all one-way functions are dead in the water, and cryptographic hashes aren’t the only ones still kicking.

Let’s examine the different address (output script) types in more detail.

Hashed Output Types

(AKA P2PKH/P2SH/P2WPKH/P2WSH)

The most commonly used type of Bitcoin address today is a pay-to-(witness)-public-key-hash address (P2PKH/P2WPKH), in which the public key is first hashed before being given to the payer. When spending this output, the owner signs the transaction and provides the raw public key so that verifiers (Bitcoin nodes) may re-hash it and compare the hash against the output script being spent.

1
OP_DUP OP_HASH160 <hash> OP_EQUALVERIFY OP_CHECKSIG

The classic P2PKH locking-script.

In P2SH and P2WSH, the address instead is the hash of a Bitcoin locking script which itself almost always contains at least one ECDSA pubkey, whose signature is required for spending. For the purposes of assessing post-quantum security, script-hash type outputs have effectively the same properties as key-hash type outputs, with the exception that P2WSH outputs are encoded as SHA256 hashes whereas all others are encoded as RMD160 hashes.

1
OP_HASH160 <hash> OP_EQUAL

The classic P2SH locking-script.

These four types of addresses currently protect the bulk of the mined and circulating Bitcoin supply.

The threat of a quantum adversary (QA) is in its ability to invert public keys into private keys. If a key-hash or script-hash address has received but not spent any of its coins, then the preimage of that hash (the key or the script) hasn’t been revealed yet. Barring out-of-band exposure (e.g. via BIP32 xpubs leaked to servers or peers), the QA generally won’t be able to attack such addresses practically.

This protection ends the moment the owner of the key/script-hash address tries to spend any of their coins. To validate a transaction spending a pay-to-*-hash output, the Bitcoin network peers must be given the key/script preimage. A quantum adversary could easily monitor these transactions and see that preimage, which always contains a public key the QA can invert. After inverting, the QA can try to double-spend the coins with a new higher-fee transaction.

Gracefully, the QA will have a limited time in which to mount this attack. A typical Bitcoin TX spends only 5 to 60 minutes of its public existence in the mempool before it is mined, at which point the coins will have moved permanently to a new address. If that new address is protected by a hash whose preimage the QA does not know, then the coins will be out of reach for the QA.

However, a significant fraction of key-hash and script-hash addresses are being reused on mainnet today. A reused address is one which receives one or more UTXOs, spends them, and having revealed their public key or spending-script, is still being used to custody additional Bitcoin UTXOs. Some estimate the amount of bitcoin held on such reused addresses was at least 5 million BTC as recently as 2019. A quantum adversary has much more time to compute the public keys exposed by these addresses. Time is on the side of the QA here; The burden of action is squarely on the shoulders of the owner to move their coins to a fresh unused address.

There is also the possibility of a large mining pool becoming a quantum adversary. Such a pool could delay mining certain transactions intentionally, to give themselves more time to crack a newly discovered public key.

Summary

P2PKH/P2SH/P2WPKH/P2WSH output script types can be reasonably secure against a QA if used properly, provided the QA needs a decent amount of processing time (more than an hour) to invert a secp256k1 public key.

The problem is that proper usage is hard. Ava Chow describes the numerous pitfalls which plague key-hashing as a countermeasure against a quantum adversary.

P2TR Outputs

In P2TR addresses, an internal public key is tweaked with a given hash to produce an output public key (where is the secp256k1 generator point). The output pubkey is then encoded directly (unhashed) in the P2TR address which receivers distribute.

When spending, the bearer can either authenticate directly by signing as the output pubkey (“key-path” spend), or they can provide the internal public key , a Bitcoin locking script, unlocking witness stack, and a proof that the locking script was committed as a merkle tree leaf of . If the script evaluation succeeds, the spender is deemed authentic (“script-path” spend). See BIP341 for more information.

The critical distinction between P2TR and the legacy pay-to-*-hash output script types is that taproot encodes a secp256k1 point directly in the output script. This means a quantum adversary (QA) can invert any P2TR output pubkey to get its secret key, and claim the P2TR UTXO using a “key-path spend”, even if the address has not been spent from before.

This is not a new observation, there has been much discourse and controversy surrounding this property of the taproot upgrade.

Summary

Against a quantum adversary, P2TR addresses are comparable in security to an already-reused key-hash address. The QA has unlimited time to invert the output pubkey and can start attacking any P2TR output from the moment they learn of its output public key . The burden of action is on the address owner to move funds to a quantum-safe address - or to avoid using the P2TR output script type - as soon as they realize the QA exists (or could exist soon).

Note on Multisig

P2SH or P2WSH addresses which use OP_CHECKMULTISIG cause a linear increase in the processing time needed for a QA to fully compromise the address. For an -of- multisig address composed of distinct pubkeys, the QA must invert at least of the constituent public keys to wield spending power over the address.

This slowdown will probably be offset by parallel-processing across multiple quantum processors, or with parallelized quantum algorithms which invert multiple public keys at once.

P2TR multisig addresses which use key aggregation do not have this property, because the taproot output pubkey can always be inverted. Possessing the secret key of is always sufficient to spend the P2TR output under current consensus rules.

Note on BIP32

Most consumer wallets derive their addresses using BIP32 hierarchical-deterministic (HD) wallet schemes. This allows a single seed to derive basically unlimited secret keys and corresponding public addresses for any script type. Wallets will sometimes share their extended public keys to avoid the need to communicate many individual child addresses.

To a quantum adversary, a BIP32 extended public key (xpub) is equivalent to its counterpart extended private key (xpriv) given enough time to invert the xpub. Once inverted, the QA can quickly derive all child addresses, and can thereafter monitor the blockchain to steal any funds paid to them.

To comply with BIP44 standards, most wallets derive one xpub/xpriv pair at specific BIP32 paths for each Bitcoin address type.

  • m/44'/0'/n' for P2PKH
  • m/49'/0'/n' for P2SH-wrapped P2WPKH
  • m/84'/0'/n' for native P2WPKH
  • m/86'/0'/n' for P2TR

Each layer of derivation in these key paths after the master key (m) is hardened, meaning that deriving that child key involves hashing the parent secret key.

Remember QAs cannot invert a hash function as efficiently as they invert elliptic curve public keys. This means that the BIP32 master key m, as well as the xprivs at any previously unused key path, are generally safe from the eyes of the QA provided the wallet has not exposed the BIP32 master public key. We will make use of this property in some of the options we discuss later.

Quantum-Safe Signatures

The critical question is: What cryptographic mechanism replaces elliptic curve digital signatures?

Whatever mechanism replaces EC signatures must be asymmetric, allowing a user to give payment instructions to a prospective sender, without surrendering control of their money to the sender. This way the receiver can claim that payment later without revealing their signing credentials to anybody (like one would with a password to a bank website). This rules out symmetric cryptographic schemes, such as HMAC, simple hashing, or symmetric encryption algorithms like AES or ChaCha.

We have numerous quantitative metrics by which to judge a replacement algorithm:

  • Public key size
  • Signature size
  • Secret key size
  • Key generation time
  • Signature computation time
  • Signature verification time

We also have qualitative statements we can make about a signing algorithm:

  • Statefulness: Does a signer need to maintain state between each signature?
  • Reusability: Can a signer reuse their secret key to sign multiple messages?

Today we’re going to explore one genre of signing algorithms which is almost certainly the safest and most conservative candidate, but which comes with some big practical issues: Hash-based signatures, or HBS for short.

Hash-based signature schemes are constructed from a simple one-way cryptographic hash function like SHA256. Secret keys are usually vectors of preimages. Public keys are usually hashes, or vectors of hashes. Signatures are usually vectors of preimages, paired with auxiliary data needed to verify the preimages correspond to a specific static public key. Unlike other candidates for post-quantum cryptography, hash-based signatures do not rely on new (possibly flawed) cryptographic assumptions - This is what makes them the conservative option.

I’ll now give a detailed description of several well-known hash-based signature algorithms, in increasing order of complexity. If I lose you in some of the math, don’t worry - Understanding the internals of the HBS schemes is not critical to understanding how they can be applied to Bitcoin.

Skip through to the final analysis section if you don’t care about the technical details of HBS schemes.

Before we begin, some notation:

Notation Meaning
The set of all possible bit strings of length
Uniform random sampling of an element from the set

Let be a secure cryptographic hash function which outputs pseudorandom bit strings of length (For SHA256, ). All constructions below are typically based on this single cryptographic primitive.

Disclaimer

I began studying these hash-based signing protocols only a few weeks ago. Do not take my technical descriptions below as precise and safe for real-world use, because I have probably made typos or omitted stuff. The purpose of these descriptions is to illustrate and convey the essence of the algorithms, not to provide any concrete implementation instructions.

Roll your own crypto at your own peril.

If you are an expert in hash-based signatures and have noticed a typo, please email me or open a pull request to fix it.

Let’s start with the simplest and earliest-known example of an HBS scheme: Lamport Signatures.

Lamport Signatures

We want to sign a single bit of information - 0 or 1 - using our hash function .

We generate two random preimages of bits each:


The tuple is a one-time secret key.

Our public key is the tuple . We can safely give the public key to anybody, and later reveal either to sign the bit zero, or to sign the bit one. Any observer with the public key can easily verify for a given bit .

We may generalize this approach to sign message strings of arbitrary bit length by generating more preimages - one per message bit. Then our secret key would be:

Each is an array of random preimages .

Our public key is made of hashes of every preimage.

To produce a signature on the message bits , we reveal the appropriate preimages per bit:

To verify, simply check that the hashed preimages match the public key for every bit in the message.

Properties

Lamport Signatures are a one-time signature (OTS) protocol - once the signer reveals a signature for a given public key, they can never use the same signing key again for a different message. If they do, the signer gives observers the ability to forge signatures on new messages they never consented to sign.

For instance, if and a signer reveals two signatures for distinct messages and , they will have now revealed all four preimages in their secret key . Any observer can now sign the other messages and even though the key owner never approved those messages.

Signatures have bit length and public keys have bit length .

Signing is simple, as it consists only of revealing secrets. Verification requires evaluations of .

Modifications

We can modify lamport signatures to improve the amount of space consumed by keys and signatures at the cost of some computation time.

Deterministic key-gen: Instead of randomly sampling our secret key preimages, we can derive them from a root secret using .

This way we only need to store a single 256-bit secret preimage for each Lamport OTS key, instead of preimages, but we do need to compute hashes to derive our public key, and we must compute hashes to sign a message of bits.

Compact public keys: We can reduce the size of public keys from to simply bits, by representing the public key itself as a hash of the standard Lamport public key.

However, we must now adjust our signature algorithm to supply not only the preimages, but also the complementary hashes, which are needed to reconstruct the public key hash .

Signatures double in size to bits, whereas public keys shrink from bits to only bits.

Verifiers can verify against by hashing each of the preimages and then hashing those hashes to re-derive .

Comparisons

The following table shows some concrete examples of time/space tradeoffs for Lamport signatures. In these examples, I’ll set , to emulate the results using the well-known hash function SHA256. All sizes are in bits.

Algorithm Signature size Public key size Secret key size
Vanilla Lamport
Compact Lamport

Below I note the time complexity of Lamport signatures in terms of the number of invocations of the hash function .

Algorithm Keygen time Signing time Verification time
Vanilla Lamport
Compact Lamport

Viability for Bitcoin

I expect the Compact Lamport signature approach would be the most practical flavor of Lamport Signatures, as public keys would be the same size or possibly smaller than a P2TR pubkey is today.

However, even the most space-efficient Lamport signatures with the lowest viable security levels () would require at least 6400 bytes of witness space per signature before compression. That’s 100x larger than a Schnorr signature.

There’s also the matter of key reuse. Lamport signatures are a one-time signature scheme. If a Bitcoin user spends from a hypothetical “pay-to-lamport-public-key” address, they’ll never be able to spend from that address again without giving observers some power to forge signatures.

Power users would not be affected greatly, as the best-practice touted by most experienced Bitcoiners is to use addresses only once, for a single receive/spend cycle. Yet, as we’ve seen earlier, a huge fraction of bitcoiners by volume have either never heard this advice, or have disregarded it. It will be difficult to convey to these users that address reuse with Lamport signatures will be more than just a privacy no-no - It could seriously compromise their security. This would make life especially difficult for cold-storage hardware signing devices, which rely on a semi-trusted host machine to prompt them with transactions to sign.

Lamport signatures are stateful, in that a signer should know if he has used his private key to sign a message before to know whether signing again could be dangerous.

Lamport signatures are not backwards compatible with Bitcoin’s consensus protocol as it exists today, although an outlandish scheme has been proposed by Ethan Heilman which make use of OP_SIZE to Lamport-sign the size of an ECDSA signature. Whether this approach is secure is still up for debate. But even with such creative invention, the size of such a signature would prohibit its usage in P2WSH addresses. At least with current knowledge, a soft-fork would be needed to add Lamport signature support.

Even after such a soft fork, existing addresses with exposed public keys would still be vulnerable to a quantum adversary. Users would need to actively migrate coins to a hypothetical pay-to-lamport-public-key address format.

Winternitz One-Time Signatures (WOTS)

Winternitz signatures rely on a chain of hashes starting from a set of secret preimages. By revealing certain intermediate hashes in that chain, the signer can sign a specific message.

In comparison to the Lamport scheme, WOTS shoulders a higher computational burden in exchange for much shorter signatures. Let’s see how they work.

First, let’s re-establish some parameters:

  • Let be the bit-length of the message we want to sign.
  • Let be the “Winternitz parameter” (used for time/space tradeoffs).
  • Let be the bit-group width into which we parse the message.
  • Let be the length of the message in digits of base .
  • Let be the checksum length in digits of base .
  • Let be the overall length of the message plus the checksum in digits of base .

As WOTS relies on hash-chains, we need a hash-chaining function which uses our primitive hash function internally.


So for instance, would hash twice.

Now we’re ready to generate our keys. We start by sampling random preimages of bits each.

To compute the Winternitz public key , we iteratively hash each preimage times.


To sign a message of bit-length , we break up into digits of base (I think of them as groups of bits).

We compute a checksum of the message:

Because , the binary representation of is at most bits long. This means we can always represent as an array of digits in base . In fact that’s exactly what we’ll do.

We append this checksum array to the message , to get the final message to sign, which is just an array of digits of base (I think of them as groups of bits).

To sign the checksummed-message , we go digit-by-digit through , and for each digit , we recursively hash the preimage , for iterations. This array of “intermediate hashes” in each hash-chain is the Winternitz signature.


A verifier given the plain message and public key must first reconstruct the checksummed message just like the signer should’ve. Then the verifier simply follows each hash chain in the signature to its expected terminal hash, and compares these terminal hashes against the public key .

If this holds for all , then the signature is valid.

Properties

Security. Note the special role played by the checksum. Without it, revealing one set of intermediate hashes should allow an observer to forge signatures on any message in a “higher” position in the hash chain.

For instance, consider the following diagramed example.

If we don’t add a checksum to the two-digit message , the signature would simply be the two intermediate hashes . But then anybody who learns this signature could forge a signature on any message “higher” in the chain, like or .

Because of the checksum construction, increasing any message digit implies decreasing at least one checksum digit . To forge the signature on the checksum as well, the observer would need to invert the hash function (implausible). So an observer cannot forge any other valid signature for as long as the signer uses their signing key only once.

Size. Signatures, public keys, and secret keys all have bit length

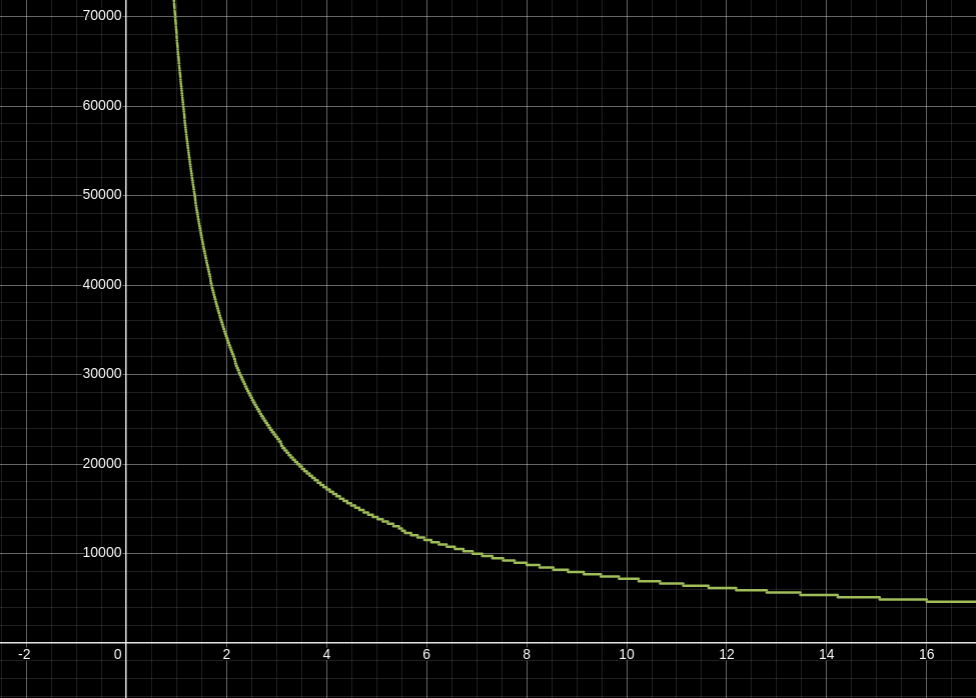
In case that equation seems unintuitive to you, you’re not alone. I plotted the relationship between the time/space tradeoff parameter on the X axis and the final WOTS signature size on the Y axis (in bits). I set to generate this particular graph.

Higher values of result in much smaller signatures and keys at first, but we get diminishing returns. In the limit as , it seems the shortest we can make our signatures is .

Approaching anywhere near that limit would be wildly impractical though, because by increasing we also exponentially increase the amount of work we need to do to generate public keys, sign messages, and verify signatures.

Runtime. Given a secret key containing preimages, to derive its public key we must compute hashes to derive our public key.

Public key generation uses the same hash-chaining procedure as signing/verifying. To sign or verify a signature, we must compute at worst hashes (on average, only half that).

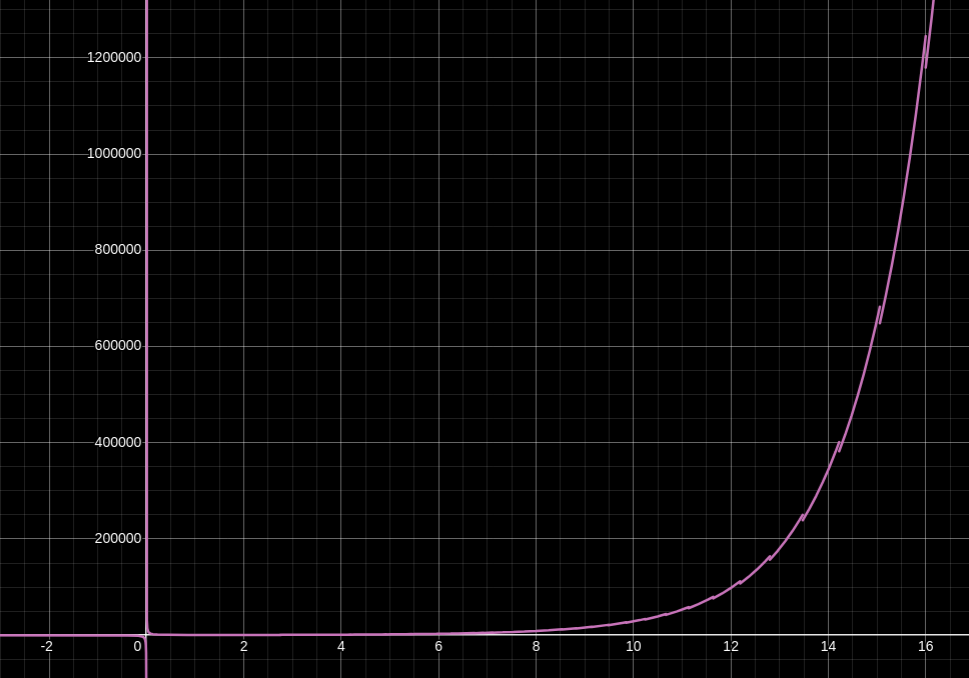
To avoid this exponential blowup in computation time, most real-world WOTS instantiations keep quite low, usually at most 16, which would mean computing on the order of hashes for a signature operation, per bits in the message. As you can see, beyond performance will become a big issue.

X-axis is , Y-axis is the number of iterations of needed to generate a public key.

For reference, my weedy little computer can generate a WOTS public key with in around 0.4 seconds. Verification and signing will each require about the same in sum, as the signer starts the hash-chain which the verifier finishes.

Curiously, due to the zero-sum nature of the hash-chain signature construction, signers and verifiers who are able to select the message they’re signing can also influence the amount of work they and their counterparty must perform. By selecting a message digit significantly lower than the base , the signer needs to do less work to compute , while the verifier must do more work to compute . This could be a hinderance for a blockchain application like Bitcoin, because one signer could disproportionately emburden thousands of verifiers (nodes).

Modifications

Compact public keys: WOTS lends itself well to compacting public keys via hashing. A Winternitz signature gives the verifier everything they need to reconstruct the signer’s public key , and so we can represent a WOTS key succinctly with its hash, in exchange for an one additional unit of work for the verifier.

This decreases the public key size from bits to merely bits.

Deterministic key-gen: Like with Lamport signatures, WOTS secret keys can be generated from a seed with only invocations of .

Smaller and more secure signatures: To improve performance and security, one should consider using WOTS+, a variant of WOTS which adjusts the hash-chain construction to XOR each of the intermediary hashes in every hash chain with a randomization vector. This odd choice allows the security proof to reduce forgeries to second preimage extraction: If someone can forge a WOTS+ signature, they can also break the second-preimage resistance of . The security of WOTS+ thus relies on weaker assumptions than standard WOTS, which assumes a forging adversary cannot break collision resistance of (easier to do than finding a second-preimage). Broadly speaking, weaker assumptions lead to better security.

This means we can get away with using WOTS+ with smaller, faster hash functions which have broken collision resistance but are still believed to be second-preimage resistant, as long as one can accept the lower security level implied by their shorter output. Or WOTS+ can be instantiated with larger hash functions, and for only a modest increase in signature size and verification complexity, we gain the added security of weaker assumptions.

WOTS+ relies on a set of -bit randomization elements and an HMAC key which can all be generated pseudorandomly with and a seed, just like the vanilla WOTS secret key .

Instead of computing the intermediate values of the hash-chains as , WOTS+ uses a keyed hash function (think of it as an HMAC). The chaining function XORs the output of each keyed-hash on with a randomization element before proceeding with the next iteration.


For instance, would be:

WOTS+ appends the tuple to the public key, so that verifiers may also compute . To improve space-efficiency for public and secret keys, we can instead derive from a public seed (which is itself probably derived from a secret seed). The signer distributes as part of their signature.

The compact WOTS+ public key can then be defined as a simple -bit hash.

More efficient signatures using brute-force compression: This paper suggests modifying the WOTS signing algorithm so that the signer repeatedly hashes the input message along with an incrementing 32-bit salt/counter , until the resulting WOTS message checksum equals some fixed static value, e.g. zero. The signer appends the salt to the signature and the verifier confirms the resulting checksum is zero.

This allows the signer to omit the checksum portion of the WOTS signature, because the checksum is verified to always work out to a fixed static value. Messages without this fixed checksum are not valid, and so the checksum itself does not need to be signed. This approach is called “WOTS with Compression” (WOTS+C).

The effect of this compression is to reduce the overall runtime of the scheme on average across keygen, verification, and signing, while also reducing signature size by removing the checksum hash chains from the construction completely. One would think signing WOTS+C would take more time, due to the signer’s brute-force search for the salt . But the signer now needs to compute only intermediate hashes for the signature, instead of . These effects offset each other. At least, it does according to the paper authors, I have not yet validated this myself.

The authors of WOTS+C even propose ways for the signer to further reduce the size of their signature by removing additional chains from their signature, at the cost of additional work to find an appropriate message salt.

Comparisons

The following table shows some concrete examples of time/space tradeoffs for various kinds of Winternitz signatures. In these examples, I’ll set , to emulate the results using the well-known hash function SHA256. All sizes are in bits.

Algorithm Signature size Public key size Secret key size
Vanilla WOTS
Compact WOTS
Compact WOTS
Compact WOTS
Compact WOTS
…
Vanilla WOTS+
Compact WOTS+
Compact WOTS+
Compact WOTS+
Compact WOTS+
…
Compact WOTS+C
Compact WOTS+C
Compact WOTS+C
Compact WOTS+C

Below I note the worst-case time complexity of each flavor of Winternitz signatures in terms of the number of invocations of the hash function (or for WOTS+).

For the sake of brevity, let be the total number of hashes in each chain.

Algorithm Keygen time Signing time Verification time
Vanilla WOTS
Compact WOTS
Vanilla WOTS+
Compact WOTS+
Compact WOTS+C *

The additional operations in Compact WOTS+ keygen are caused by derivation of .

* is the number of possible message hashes which result in a zero checksum. See page 6 of the SPHINCS+C paper.

Viability for Bitcoin

Winternitz signatures are significantly smaller than Lamport signatures. With compaction and deterministic key-generation, the public and private keys can be condensed down to the same constant size ( bits).

Compact WOTS+ with seem like the best compromise between speed and signature size. Assuming we use SHA256 as our hash function, WOTS+ with could be instantiated with signatures of size slightly more than 1KB, with 32-byte public and private keys. Verification would require at most 8670 hash invocations, which takes only a few milliseconds on most modern machines. WOTS+C could be used to compress signatures even further, and verification can be parallelized across hash chains since they are independent.

However, like Lamport signatures, WOTS is a stateful one-time signature scheme, so it inherits all the same security concerns as Lamport signatures regarding address reuse ergonomics.

Hash to Obtain Random Subsets (HORS)

HORS is a few-time signature protocol based on Lamport Signatures which relies on complexity theory to make signatures smaller and provably resilient to forgery.

To generate a HORS key, the signer samples some large number random preimages , and gives out the hashes of those preimages as their public key .


To sign a specific message, the signer reveals a specific subset of preimages. Which subset to reveal is dictated by the message to sign.

tells us the total number of preimages in the secret key, while is the number of selected preimages per signature. Notice there’s a space tradeoff between HORS signature and pubkey size. Increasing means larger signatures. Increasing means larger public and private keys.

These parameters also affect the security of the HORS scheme. With total preimages, we have possible unordered combinations of preimages - This is the number of possible signatures. If we have a message space bits wide, we should choose and so that ; otherwise there would be collisions where one signature is valid for more than one message.

The key ingredient of HORS is a subset selection algorithm . Given a message , this function returns a unique subset of random elements in the set

The HORS paper suggests two bijective functions which fulfill the subset-selection role of with perfect OTS security, ensuring that each message uniquely corresponds to a -element subset of .

However these bijective functions are not one-way functions, so if a signer provides two or more signatures from the same key it is trivial for an observer to forge new signatures by working backwards to determine which messages they can now sign using the signer’s revealed preimages.

To address this, HORS instead uses a one-way hashing function to select subsets - hence the name Hash-to-Obtain-Random-Subsets. Here’s how you might implement . The signer computes the hash of the input message , and then parses into -bit integers . The output of is an bit string, so this gives us at most bit groups per message hash, but we can extend the output of to arbitrary lengths (e.g. by chaining it) so this isn’t really a hard limit.

Because the output of is pseudorandom, it’s possible that the integer set we parse from it could contain duplicate elements. If this occurs, we simply discard the duplicates and allow for shorter signatures. So really HORS signatures contain at most preimages, but possibly fewer. The lower is, the more likely duplicates are to occur. This actually has been the subject of certain attacks in which the attacker intentionally tries to find messages for which the set is small, so that they don’t need as many preimages to forge a signature.

After computing , the HORS signer maps the integers to a subset of their secret key preimages. This forms the signature on message .


A HORS verifier with a public key can then verify the message by recomputing as the signer did, and checking for each preimage in .

Properties

Unlike previous signature schemes, using a HORS signing key to sign more than one message does not immediately compromise the key’s security, it merely reduces security. An attacker who sees two or more signatures from the same secret key will need to brute-force the hash function to figure out which alternative messages they can forge signatures on using the revealed preimages. This is why HORS is designated a “few-time” signature (FTS) scheme, instead of a one-time signature (OTS) scheme. The hash-to-subset approach is what enables the few-time property of HORS.

The signer still has to be cautious though, because as the attacker sees more signatures, their guess-and-check attack will get progressively easier. The HORS paper describes exactly how much easier. The following expression gives the bits of security for a HORS public key after an attacker has seen distinct message signatures.

Usually is small (less than 10 signatures) but can be increased relatively safely by also increasing either or . This quickly blows up the size of keys and signatures though.

Size. HORS signatures have bit size , while public and private keys have bit size .

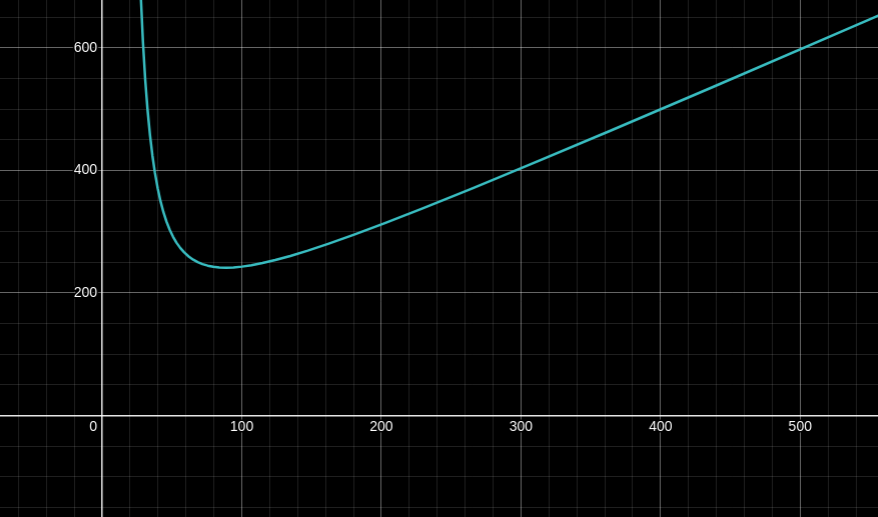
If we fix (so ), and we fix a constant security level of bits, then we can plot the key size as a function of signature size .

X axis is the signature size . Y axis is the key size . Exercise to the reader: How would you use this information to deduce the smallest possible combined key + signature size which still achieves bits of security?

Runtime. The HORS keygen procedure requires evaluations of the hash function . Signing is extremely fast, just a single evaluation of the subset selection algorithm , and then the signature elements are picked from a set of preimages the signer already knows. Verification is also fast, with just invocations of , and is usually much lower than .

Modifications

Deterministic key-gen: As with previous examples, we can derive the HORS secret key preimages from a single -bit seed. This reduces secret key size to bits but at the cost of additional hash invocations during key generation.

Compact public keys: A modified version of HORS called “HORS with Trees” (HORST) was proposed by the authors of the SPHINCS signature scheme. Instead of representing the public key plainly as hashes each of bits, the public key is defined as the merkle-tree root of those hashes. Signatures must be lengthened to supply merkle-tree membership proofs for each element of the signature , but this trade-off greatly decreases the public key length from bits to only bits.

Comparisons

The following table shows some concrete examples of time/space trade-offs for HORS signatures. In these examples, I’ll aim for a security level of approximately bits when (one signature). The hashed message size will vary to accommodate different parameters. All sizes are in bits.

Algorithm Signature size Public key size Secret key size
Vanilla HORS ,
Vanilla HORS ,
Vanilla HORS ,
Vanilla HORS ,
Vanilla HORS ,
Vanilla HORS ,
Vanilla HORS ,
Compact HORST , *
Compact HORST , *
Compact HORST , *
Compact HORST , *
Compact HORST , *
Compact HORST , *
Compact HORST , *

Below I note the time complexity of HORS signatures in terms of the number of invocations of the hash function .

Algorithm Keygen time Signing time Verification time
Vanilla HORS
Compact HORST *

The exact amount of bits by which the HORST signature size grows (and thus verification time as well) is determined by the function (see page 9 of the SPHINCS paper for more info).

Viability for Bitcoin

HORS is conceptually refreshing, because it demonstrates that hash-based signatures can be quantifiably secure even when secret keys are reused. Since Bitcoin signing keys are typically only used a few dozen times at most, a few-time signature scheme like HORS might be acceptable for the vast majority of Bitcoin use cases, especially if each signature decreases security by a predictable and incremental amount, rather than the all-or-nothing security risks of reusing an OTS secret key (like with WOTS or Lamport).

However Vanilla HORS compromises significantly on public key sizes, while the more compact HORST experiences huge increases in signature key sizes as a trade-off. By comparison, Compact WOTS provided public keys of the same size with signatures roughly a quarter of the signature size HORST has. Safely supporting additional signatures () would require even larger signatures.

HORS is not a stateful signature scheme, but the signer should know roughly how many times they have used a given key pair so that they can avoid over-exposing their key. On the coattails of this assumption ride the same security issues as WOTS and Lamport signatures regarding address reuse in a Bitcoin context. The problem with HORST is really that to make a key secure for reasonably large numbers of signatures, we must make our parameters very large which inflates either the keygen/signing runtime, or the signature size.

Forest of Random Subsets (FORS)

FORS is another few-time signature scheme based on HORST (discussed above). It was first introduced as a component within the SPHINCS+ paper in 2017, but it deserves a definition on its own as it improves on HORST to reduce signature sizes dramatically.

The primary distinction between HORST and FORS is that FORS public keys are represented as the hash of several merkle trees - hence the use of the term “forest”. Each leaf node of these trees is, like HORST, the hash of a secret preimage, and we sign data by revealing specific preimages along with their merkle tree membership proofs.

Let be the number of merkle trees and let be the number of preimages in each tree, for a total of preimages. The trees will all have height .

This construction gives us merkle tree root hashes . We hash these roots to derive the FORS public key .

To sign a message , we hash using a randomized subset-selection algorithm to obtain where each digit (as in HORST). But whereas HORST uses those digits as indexes into a single tree, FORS uses those digits as indexes into separate merkle trees - one index per tree - to select which preimage to reveal from each tree. This ensures that FORS signatures always have a constant size (unlike HORS or HORST).

FORS is designed to generate the secret preimages from a small seed, giving constant secret key size. Given a secret FORS seed we can compute the -th preimage as . After computing , we can group these preimages into sets of length , and then construct the merkle trees from them.

Safety Notice: FORS is designed to use tweaked hash functions which prevent multi-target attacks where an adversary can exploit precomputation to do a drag-net attack on multiple keys in parallel. Do not naively implement FORS without properly tweaking (namespacing) each hash invocation. This risk applies to HORS and other signature schemes as well, but was not well understood until recently.

Note especially that the subset selection algorithm must be tweaked with a secret value, to prevent adaptive chosen-message attackers from selecting messages which would trick the signer into revealing specific preimages desired by the attacker. Reference.

Properties

Security. Like its predecessors, FORS is a few-time scheme which means the signer can confidently quantify the security of their public key even after revealing some signatures. The bit security of a FORS public key against a signature forging attack (with attacker-chosen messages) after revealing signatures is:

Source

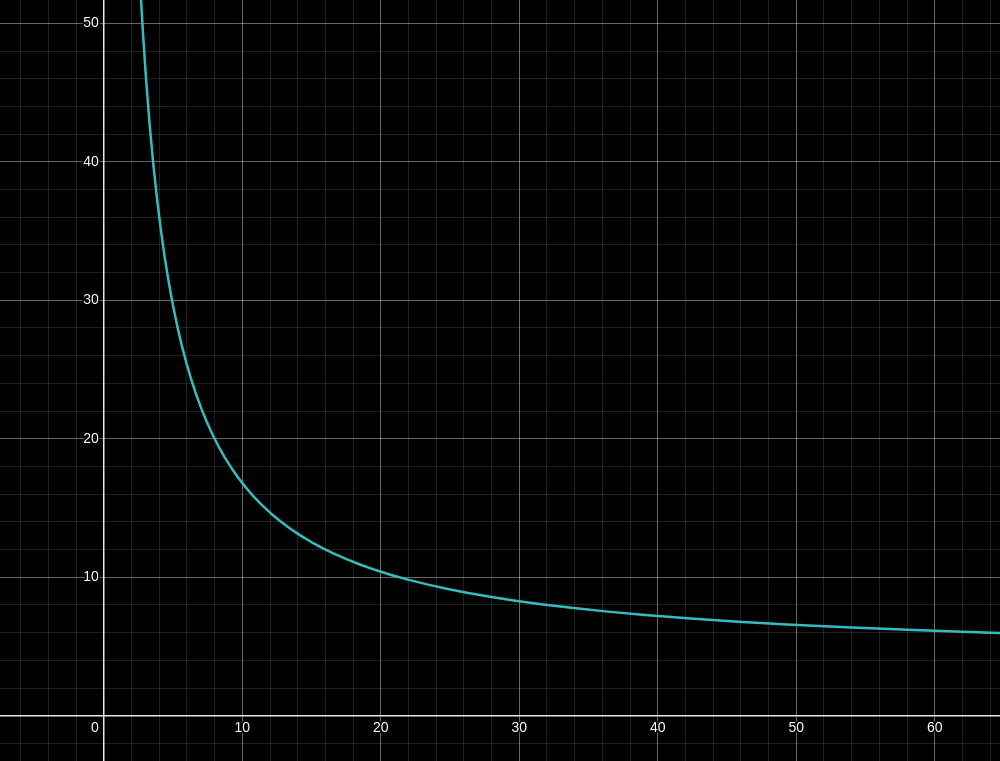
By fixing a security level of bits given signatures, we can compute the required tree height as a function of the number of trees in the “forest”.

X axis is (number of trees). The Y axis is (height of each tree). This graph was computed with and (i.e. 128 bits of security after 128 signatures)

For instance, with trees and signatures, we would need trees of height , for a total of preimages.

Size. Public and secret FORS keys are both a constant size of bits each.

A FORS signature consists of preimages, plus merkle tree proofs containing hashes each, for a total of bits per signature.

Runtime. Key generation requires deriving secret preimages, hashing preimages, and then computing merkle tree roots therefrom. With one final hash to compress the merkle roots into the public key, this gives a total key-gen runtime of:

Signing requires a call to (presumably a single hash invocation) to select which preimages to reveal, along with constructing merkle-tree membership proofs. If a signer can cache the internal nodes of the merkle trees in memory, they can compute a signature with only a single invocation of .

If on the other hand the signer starts from just the seed (pre-keygen), then to construct a merkle proof for a single tree, they must first derive the preimages for that tree. Then they recompute hashes on level 0 of a tree, then hashes on level 1, then hashes on level 2, and so on until level where they only need to compute a single hash, finally arriving at the merkle root of the tree. Expressed more generally, this would require invocations of per merkle proof. The signer must construct merkle proofs, so the total worst-case signer runtime is:

The verifier’s runtime is much smaller. The verifier must run to compute the selected preimage indexes. They must hash each of the preimages from the signature, and verify the merkle proofs with hash invocations each. With one final hash to compute the expected signer’s pubkey, this gives a total verifier runtime of:

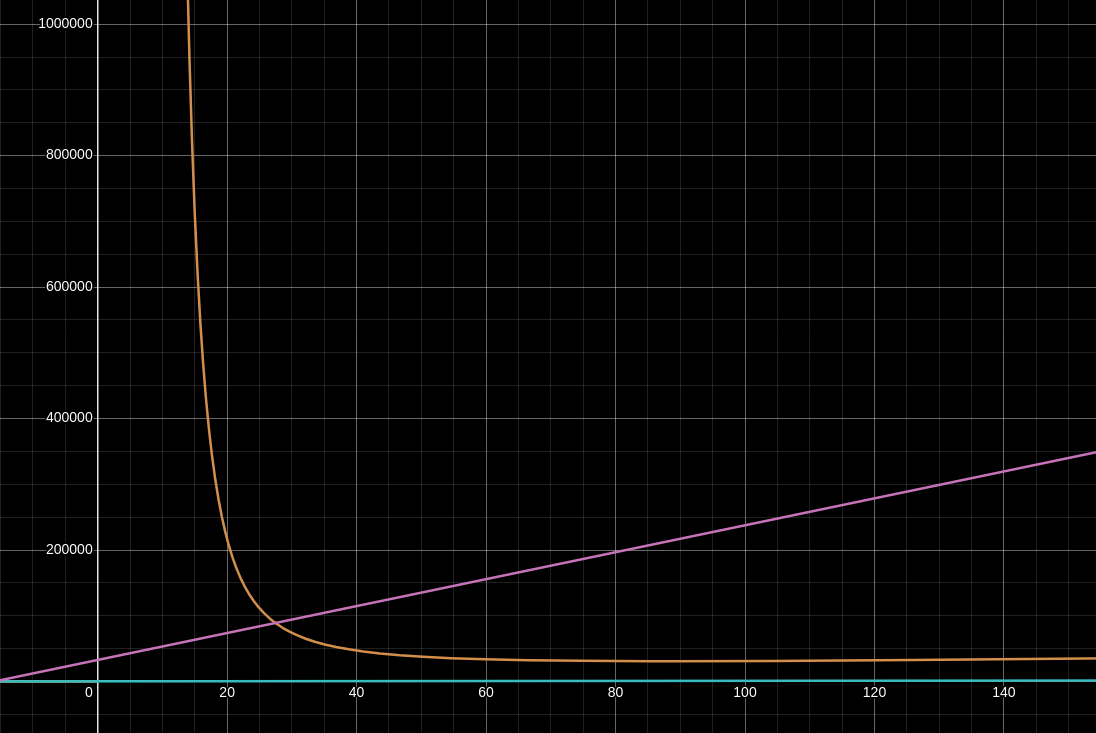
Check out the following graph which compares the time/space performance of FORS signatures. For this visualization, I fixed the FORS security parameters and (i.e. 128 bits of security expected after 128 signatures), with a hash output size of .

Along the X axis is an input , for the number of FORS trees. The tree height is computed as before as a function of to achieve our desired security level.

  • The orange curve is , representing the total number of preimages the signer must generate and hash into their public key. This curve is directly proportional to both key-generation runtime and signer runtime (or memory usage if caching is used), but it does not affect public/secret key size.
  • The pink line is the signature bit-size , which grows linearly with .
  • The blue line hugging the X axis is the verifier’s runtime . It grows linearly with , but for all reasonable choices of the verifier needs to evaluate at most a thousand hashes or so.

This suggests that for the and parameters we fixed here, we likely would want to set . Any lower, and signers would experience an exponential runtime blowup. Any higher and we get diminishing returns in signer runtime savings.

Playing around with the parameters a little, we can see that using fewer but larger trees (lower w/ higher ) gives signers another advantage besides small signatures. Like with HORS, lower means fewer preimages revealed per signature, which means the security bit-level decreases more slowly as signatures are revealed.

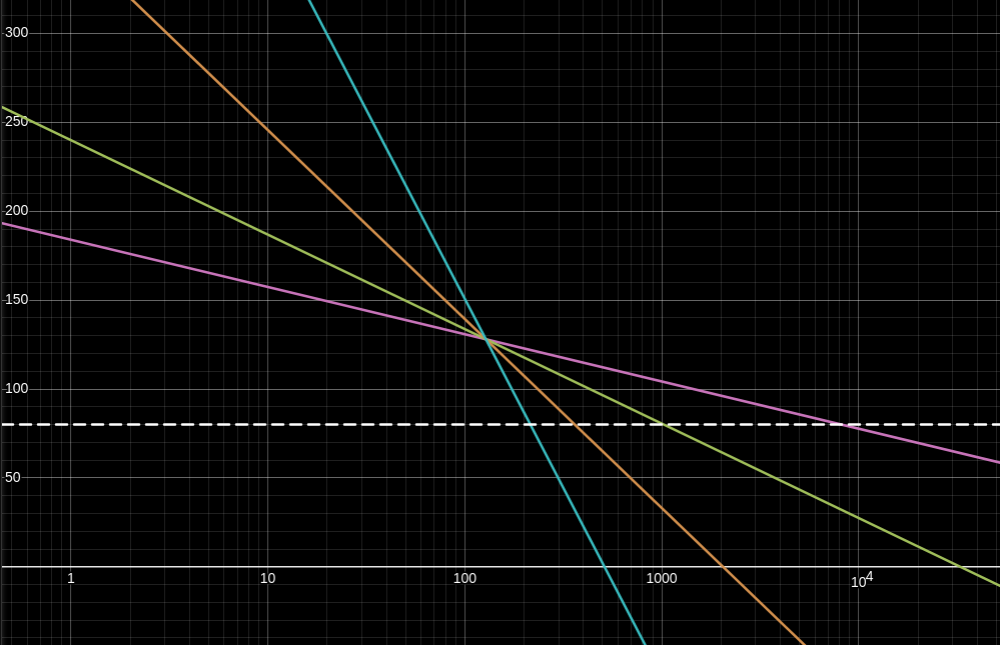
See the following visualization with as an input on the logarithmic-scale X axis.

On the Y axis is the expected security level after signatures. The different lines represent the declining security of different FORS parameter sets. FORS tree heights were computed with setting and (same as before), but this graph shows what happens before and after a signer has issued their 128 signatures.

  • The pink line is FORS with , .
  • The green line is FORS with , .
  • The orange line is FORS with , .
  • The blue line is FORS with , .
  • The white dashed line is bits of security, which represents an approximate boundary below which forgery might be practically achievable for currently available hardware.

Note how the FORS signer (pink line) can create almost signatures before their key’s expected security drops below 80 bits. At the opposite extreme, the signer (blue line) can only create 214 signatures before crossing the same boundary. Even though the tree height was computed the same way for all four signers, the security of signers with fewer trees decreases much more slowly.

Modifications

Security against adaptive chosen-message attacks: The authors of this paper suggest modifying the FORS signing algorithm to make the subset-selection function dependent on the signature itself, using a chain. They call this algorithm “Dynamic FORS” (DFORS). But they also note that a simple pseudorandom salt as used in SPHINCS+ is sufficient for safety against adaptive chosen-message attacks. As such I have elected not to go into detail as the DFORS modification seems unnecessary.

More efficient signatures using brute-force compression: This paper suggests modifying the FORS signing algorithm so that the signer repeatedly hashes the input message along with an incrementing 32-bit salt/counter , until outputs a set of index digits with a trailing zero digit at the end (i.e. the last bits of the salted message hash are zero). The signer can then FORS-sign the set of digits , omitting , and including the salt in their signature. The verifier recomputes and checks the final digit matches the requirement .

Because is also enforced by the verifier, the signer can omit the last preimage and merkle proof on from the signature, as that digit of the message is presumed static (A message which never changes does not need to be signed). Indeed the signer doesn’t need to even have a final -th tree.

The effect of this modification is to reduce signatures size by approximately bits, and reduce signing/verifying runtime as well (though I have not verified the runtime-reduction claim). The authors call this modification “FORS with compression” (FORS+C).

The authors have also noted that if the signer wishes to further reduce signature size, they can perform additional work to reduce the size of the 2nd-to-last tree by forcing more trailing bits to hash to zero.

Intuitively, this compression mechanism has a larger impact when the trees are larger (when is larger), because pruning the last tree from the signature construction makes a comparatively larger impact. Of course the trade-off is that we must do more work to find a salt which produces a message hash with trailing zero bits. On average to find a hash with trailing zeros, we must compute hashes, with hash invocations at the very worst.

Smaller signatures using Winternitz chains: This paper suggests extending the leaves of each FORS tree with a chain of hashes, much like the Winternitz OTS scheme. This extra dimension gives a new parameter, the length of the Winternitz chains , with which to expand the space of possible signatures. Now signatures are composed of intermediate hashes within the chains hanging from the FORS tree leaves.

More possible signatures for the same size message means in theory that signatures should be more secure. This modified scheme is called “Forest of Random Chains” (FORC). One could think of standard FORS as a FORC instance with chains of length .

The authors demonstrate that this extension improves reduces probability of two signatures colliding within a tree from (one chance per leaf) with standard FORS, to with FORC, where is the length of the Winternitz chains.

Unfortunately the FORC authors did not provide an explicit formula for the bit-security of FORC after signatures, so we will have to work that out for ourselves.

Click here to see my derivation

Recall the FORS security level of bits over all trees after signatures:

Convert this to the probability that signatures allow a forgery:

With FORC, the inner per-tree probability (the chance of preimage indexes colliding within a tree) is multiplied by the factor .

Converting back from a probability into bits of security:

Use the logarithm identities and :

Thus, the bits of security we receive by extending the leaves of a FORS tree with Winternitz chains of length is exactly . This improves on standard FORS by exactly bits, which evaluates to zero if .

After working it out, FORC’s security level is bits .

This improves on standard FORS by exactly bits, which evaluates to zero if .

For a given set of security parameters and we can compute a surface in a 3-dimensional FORC configuration space. I’m too lazy to diagram it, sorry, you’ll have to get imaginative. This surface represents the possible choices for which fulfill those security parameters. The security earnings from higher values of can be exploited to achieve the same level of security with smaller or fewer FORS trees.

The savings diminish quickly as grows though. It seems like is about the limit of usefulness beyond which the security savings earn little in terms of signature size reduction. The majority of savings are earned by the first few hashes in the chains. Winternitz chains with as few as hashes can reduce signature sizes by several thousand bits.

In exchange for these security/size savings, FORC signers must process the hash chains for each of the FORS leaves. Keygen and signing runtime is multiplied by a factor of , as the signer must now compute hash invocations per leaf instead of just 1. Verification is slowed by (at worst) extra hash invocations, which can be minimized with reasonable choices of and .

Comparisons

The following table shows some concrete examples of time/space trade-offs for FORS signatures. In these examples, we will fix a security level of bits after different numbers of signatures. The output size of the primitive hash function is set to bits, and all sizes are also listed in bits.

Algorithm Signature size Public key size Secret key size
FORS , ,
FORS , ,
FORS , ,
FORS , ,
…
FORS+C , ,
FORS+C , ,
FORS+C , ,
FORS+C , ,
…
FORS , ,
FORS , ,
FORS , ,
FORS , ,
…
FORS+C , ,
FORS+C , ,
FORS+C , ,
FORS+C , ,
…
FORS , ,
FORS , ,
FORS , ,
FORS , ,
…
FORS+C , ,
FORS+C , ,
FORS+C , ,
FORS+C , ,

I have omitted concrete sizes for the FORC variant of FORS, as they would not be fairly comparable. We would need to use a slightly higher or slightly lower security bit-level , in order to fix integer parameters for and . FORC signature sizes are comparable to FORS+C: A little smaller for some parameter sets, a little larger for others.

Below I note the time complexity of FORS signatures in terms of the number of invocations of the hash function .

Algorithm Keygen time Signing time (worst case) Verification time
FORS
FORS+C
FORC

Viability for Bitcoin

The FORS protocol allows for much more robust keys than HORST. The same size signatures provide much stronger few-time security, permitting more signatures per key before exhaustion. FORS is also a well-studied protocol, with many variants and higher-level protocols based on it.

This few-time scheme might be a possible candidate for usage on Bitcoin, if but for the large signature sizes. Even the smallest FORS+C signature with , , , still results in a signature which is 4256 bytes long, 66x the size of a BIP340 Schnorr signature, and 4x the size of a WOTS signature (albeit with much cheaper verification and viable multi-use security). The compression afforded by FORS+C is significant but ultimately cannot compete with traditional ECC.

Combining the principles of FORS+C and FORC could result in smaller signatures and merits further investigation, but this seems unlikely to shave more than beyond a few thousand bits off of each signature.

Merkle Signature Scheme (MSS)

MSS is our first example of a “many-time” signature (MTS) scheme, in contrast to the one-time or few-time schemes we’ve seen until now. It was first proposed by Ralph Merkle in 1979 (the same man after whom the “merkle tree” data structure itself is named).

The remarkably simple premise of MSS is this: By unifying many one-time signature (OTS) public keys as the leaves of a merkle tree, we can use each OTS key only once, but succinctly prove any OTS key’s membership in the merkle tree’s root hash. Our master public key is then defined to be the root hash of this merkle tree. If is the height of the merkle tree, then the signer may produce up to signatures valid under that public key.

The signer first samples random OTS private keys , and computes their public keys . The hashes of those public keys are then used as leaf nodes to construct a merkle tree root , which is finally used as the MSS public key.

There are many flavors of MSS, the most well-known of which being the Extended Merkle Signature Scheme, or XMSS, which instantiates MSS using Winternitz as its one-time signature scheme. The next candidate protocol, SPHINCS, may also be argued to be an instantiation of MSS, though SPHINCS is so radically evolved from Merkle’s original scheme that it might be best to group it into a completely separate class of its own.

Due to the promising candidate which follows, I will omit any specific long-winded protocol explanations here. If you would like a detailed example of an MSS protocol, I highly recommend reading the XMSS paper.

Viability for Bitcoin

Although MSS schemes give us our first tantalizing glimpse at truly scalable hash-based signatures, they still suffer from the effects of statefulness. To safely use any Merkle Signature Scheme, the signer must always remember which leaf OTS keys they have or have not used - usually implemented with a simple counter. If they lose this state, the signer cannot safely continue using the key. If the signer were to issue more than one MSS signature with the same state, it could compromise the leaf OTS key, which in turn compromises the whole key.

However, the principle of MSS is incredibly flexible, which is why so many modern hash-based signature protocols are based on the core ideas of MSS, including the next one.

SPINCS+

SPHINCS+ is a state-of-the-art hash-based signature system which leverages concepts from the previous signature schemes I’ve described earlier. SPHINCS+ is currently the only hash-based signature (HBS) protocol to have been finalized by NIST as an approved post-quantum digital signature standard. In NIST’s terminology, SPHINCS is referred to as “SLH-DSA”, or “StateLess Hash-based Digital Signature Algorithm”. You see, SPHINCS is also special because unlike most many-time signature (MTS) schemes which use hashes, SPHINCS does not require signers to keep state.

SPHINCS+ key-generation starts from three secret random values:

The signer constructs their public key by building an MSS tree deterministically from , where each leaf is a WOTS+ public key. If the tree has height then the signer must derive WOTS+ secret keys. The root hash of that tree, , along with , is the SPHINCS+ public key.

If one were to use these WOTS+ keys to simply sign messages directly, then this is just a particular flavor of MSS, but SPHINCS takes things further.

Instead of signing messages, each of the WOTS+ leaf keys are used to certify a child MSS tree, each of whose leaves are also WOTS+ public keys, and so on, eventually terminating after trees with a set of leaves. The higher-order tree-of-trees is typically referred to as the “hyper-tree” (bonus points for cool-sounding jargon) and its overall height summing the height of all internal trees and the root tree is . The height of each internal tree in the hyper-tree is .

The advantage of this approach, rather than a simple MSS tree, is that to sign a message with the bottom-level leaves of the hyper-tree, the signer does not need to re-derive the entire hyper-tree - they only need to derive the specific certified trees along the path from leaf to root. All other trees can be ignored.

The final leaf WOTS+ keypairs could be used to sign messages directly, but SPHINCS uses them instead as a final certification layer to sign a set of FTS keypairs. Specifically with the modern NIST-approved SPHINCS+ variant, those final FTS keypairs use the Forest of Random Subsets (FORS) algorithm, which we discussed earlier.

The entire SPHINCS+ signature is a package, consisting of:

  • a FORS signature on the actual message
  • WOTS+ certification signatures
  • merkle tree membership proofs - one for each WOTS+ certification pubkey
  • a randomizer (explained below)

See the following diagrammed example with and . To sign a given message, the signer only needs to re-derive three trees with four keys each. His total tree has height , and so he actually has possible leaf keys available to sign with. The signer doesn’t need to re-derive most of them because they are located in hidden trees which are irrelevant to the particular leaf key he is signing with.

The components of the SPHINCS signature (plus the message) allow a verifier to reconstruct the root node of the hypertree, which is then compared to the root tree node hash in the SPHINCS public key, .

why mix two signing algorithms? why not use only FORS?

SPHINCS uses WOTS+ to certify intermediate trees (and FORS keys), because WOTS+ provides very small signatures as far as HBS schemes go. Depending on the number of layers in the hypertree, we may need several WOTS+ certification signatures, so keeping them small is very beneficial. The fact that WOTS+ is a one-time signature scheme is not a problem, because the trees and keys we use WOTS+ to certify are generated deterministically from . Each time we sign a message, we re-derive a specific set of keys and trees, and so no WOTS+ key pair will ever be used to certify two different trees (or two different FORS keys).

SPHINCS is entirely deterministic once the initial key seed values have been generated. This includes the selection of which FORS key to sign with. When we are given a message , we compute an -bit randomizer from our secret PRF (pseudorandom-function) seed. Then we use a special hash function to compute both the message digest and the address of the FORS key we will use to sign it.

The randomizer is added to the SPHINCS signature, so that the verifier can recompute .

Properties

SPHINCS sounds like it should be a stateful signature scheme - After all the signature on the actual message is issued with a few-time signature protocol, FORS, so ought not signers to know roughly how many times to use each FTS key pair?

But actually SPHINCS is advertised as a stateless signing protocol. You see, if they increase the overall height of the hyper-tree - often to as much as 64 - a SPHINCS signer will have so many FORS keys at its disposal that picking one at random for every signature will result in a statistically negligible likelihood of key reuse. And even if by severe bad luck one does happen to reuse a FORS key, the few-time security of FORS makes it still extremely unlikely that the two FORS signatures could be used to create a forgery.

We can afford to increase the height of the hypertree this large because of the key-certification trick which saves us from re-deriving all leaf FTS. Even with heavy use, most of the possible FTS keys are never even derived, let alone used. But the fact that they could be used allows for this probabilistic statelessness property.

The modern SPHINCS+ variant of SPHINCS specifically has very small public and secret keys. Pubkeys are only bits, while secret keys are bits.

However SPHINCS signatures are very large. Exact sizes depend on a large number of parameters:

  • Security parameter (hash output size)
  • SPHINCS parameters and
  • WOTS+ parameters and
  • FORS parameters and

The total SPHINCS+ signature size is given by:

Reference (see page 36).

For different parameter sets, this can result in signatures varying in size from 8 kilobytes with the lowest security parameters up to 49 kilobytes for the highest security. See page 43 of the FIPS standard for concrete parameter sets recommended by NIST and their resulting signature sizes.

Viability for Bitcoin

SPHINCS is extremely powerful, and has numerous advantages. Stateless signing would make it a drop-in replacement for existing signature algorithms like Schnorr, so signers would not need to think about exhausting a key or tracking signature counters. The fact that SPHINCS+ is a fully standardized, open source and NIST-recommended signing algorithm would lend more credibility to arguments for adoption.

In the recommended parameter sets, NIST sets which creates so many FORS leaf keys that one could sign billions of messages per second for decades and still never use the same FORS key twice. This is the point of SPHINCS’s trade-offs in signature size and complexity: to permit signers to reuse public keys like this, issuing billions of signatures, with no meaningful loss of security.

Not even the most heavily used public keys in Bitcoin’s history have signed so many transactions… Except perhaps for the context of the Lightning network, where 2-of-2 multisignature contract participants sign sometimes hundreds of commitment transactions per minute - Though the Bitcoin blockchain rarely ever sees these transactions publicly (perhaps this fact might be useful).

However, SPHINCS’s downfall is its huge signature size. Even the smallest SPHINCS signatures with 128 bit security are around double the size of a FORS signature, and over 100x the size of BIP340 Schnorr.

Analysis

Some of the more modern hash-based signature schemes described above fulfill the hard requirements of Bitcoin:

  • Small public and secret keys
  • Fast signature verification time

Namely those schemes are:

  • WOTS / WOTS+ / WOTS+C (OTS)
  • FORS / FORS+C (FTS)
  • SPHINCS+ (MTS)

The primary trade-off points between these schemes are:

  • Signing and key generation runtime performance
  • Signature size
  • Number of signatures a signer may safely publish before forgeries become feasible

Here is a brief example to demonstrate scaling problems with hash-based signatures. If every transaction in a Bitcoin block were small-as-possible 1-input-1-output transactions (about 320 weight units before witness data), and each of those transactions used a single signature as their input’s witness, then Bitcoin’s block size limit of 4,000,000 weight units would be exhausted by:

  • 490 transactions if they each used a SPHINCS+128 signature of 7856 witness bytes, or
  • 875 transactions if they each used a FORS+C signature of 4256 witness bytes, or
  • 2976 transactions if they each used a WOTS+C signature of 1028 witness bytes, or
  • 10000+ transactions if they each used a BIP340 signature of 64 witness bytes

As of writing, blocks mined today are generally filled with some 3000-5000 transactions each, many of which spend large numbers of inputs.

It seems clear that using hash-based signatures of any kind would necessitate either a significant decrease in overall network throughput, or a significant increase in block size. The increase in block size could be pruned though, as large hash-based signatures could be attached as part of the segregated block witness and not the raw blocks themselves.

Upgrading Bitcoin

None of the above schemes matter unless it can be applied to build a real quantum-resistant upgrade to Bitcoin. In this section, I’ll propose one potential option for upgrading Bitcoin to use post-quantum hash-based cryptography while maintaining compatibility with existing elliptic-curve crypto (ECC) for as long as possible (to minimize performance loss over time).

I am not necessarily advocating to upgrade Bitcoin to use HBS in this particular way; I am merely trying to demonstrate what one possible realistic quantum resistance upgrade to Bitcoin might look like, knowing what I know today. There are far smarter people than me also working on this problem, who will probably have much to say about the methods I describe here.

UPDATE 2024-12-16

Speaking of smarter people than I, Matt Corallo has kindly done us all the favor of making an even better design for a post-quantum upgrade than my idea below (DASK). I would prefer his approach, but with a more succinct and simple hash-based signature scheme like WOTS or FORS. That said, I’ve left my original proposal below untouched outside this little update blurb.

Digests as Secret Keys (DASK)

Digests as Secret Keys (DASK) is my invented name (feat. a pronounceable acronym) for a hypothetical quantum-resistant upgrade path for Bitcoin. As far as I know, nobody else has proposed this idea before, but I would love to be proven wrong. Whether this idea is feasible or not, I would hope at least that I’m not alone.

DASK does not require any immediate consensus changes, but instead encourages a client-side specification change, modifying the way Bitcoin wallets derive their EC secret keys. A consensus change would be required later to retroactively change spending rules, and users would need to migrate their coins to a DASK-supported wallet before that fork, but the on-chain output scripts to which coins are paid would not change, so DASK would not impact Bitcoin’s fungibility, scalability, or consensus rules in the way a brand new output script format would.

Until the DASK consensus change is activated, Bitcoin transactions using EC signatures would look exactly the same as they do today. If large quantum computers never materialize for some reason, DASK need never be activated.

Background

A Bitcoin wallet is typically derived from a secret seed encoded as a mnemonic phrase. The wallet software uses the BIP32 and BIP44 standards to derive child secret/public key pairs from this seed, using a system of hashing and additive tweaking.

I am oversimplifying here, but basically the wallet starts with a secret key and a chain code . To compute a child secret-key / chain-code tuple , we hash the parent key/code with a 32-bit integer , adding the resulting hash on top of the parent secret key.*

* This describes hardened BIP32 derivation. Unhardened derivation hashes the public key instead of the secret key.

BIP32 encourages wallets to do this recursively, generating a large tree of practically unlimited size and depth, so that clients will never run out of available fresh signing keys. Once a suitable child secret key is derived, the wallet will typically use the EC secret key to compute an EC public key , and then compute an address of some format (e.g. P2PKH/P2WPKH/P2TR) based on .

DASK Description

The idea of Digests as Secret Keys is to derive a hash-based signature algorithm pubkey (or a hash thereof) and use that in place of the elliptic curve secret key . Instead of BIP32, these keys are derived using a hash-based deterministic algorithm (like with FORS or SPHINCS) from the BIP39 seed.

For example, let’s say we compute as a FORS public key: We sample our preimages, construct merkle trees from them, and compute as the hash of the forest’s roots. We can then interpret as an EC secret key, and use it to issue ECDSA or Schnorr signatures for the public key .

A simplified diagram of the DASK concept. Further layers of derivation after the BIP39 seed and before HBS keys would likely be needed for versioning and compatibility.

why?

This approach gives us a fallback option to authenticate a user in the event a quantum adversary appears who can invert our EC public key into our “secret key” . The QA can find , but is itself an HBS public key, which the QA cannot invert.

In a post-quantum world, the Bitcoin network can activate a consensus change which enforces new hash-based spending rules on all addresses: disable ECDSA/Schnorr, and instead require a signature from the HBS public key .

Since FORS, WOTS, and other HBS verification algorithms typically involve recomputing a specific hash digest and comparing that to the HBS public key, a verifying Bitcoin node could recompute the EC secret key from the hash-based signature, and then recompute , to compare against whatever output script is being unlocked.

Think of the outer EC pubkey as the outer wall or moat of a castle, and the inner HBS pubkey as the inner sanctum or keep: A highly secure fallback location, where one may safely retreat to if the first line of defense were to be breached.

Kenilworth Castle Reconstruction. Source.

The exception to the above is taproot, where an output public key is typically additively tweaked with a hash of an internal key . DASK would not work out-of-the-box with P2TR, because whatever HBS key the verifier computes from the HBS signature may not be the correct discrete log (secret key) of the actual curve point (pubkey) encoded in the P2TR output script. The verifier must also know the tapscript merkle root such that they can compute .

There are various ways we could handle this, the most obvious being to simply append the tapscript MAST root to the HBS signature witness in some way. For most P2TR users, would just be an empty string.

Until Q-Day, Bitcoin users would be free to continue signing with ECDSA and Schnorr exactly as they do today. After Q-Day, the fallback HBS mechanism would allow a straightforward and secure way for users to retain control over their money.

Benefits

The main benefit of DASK is that the Bitcoin network does not need to implement any consensus changes today. Instead a client-side spec for DASK would be needed, and then users can opt into DASK-supported wallets at their leisure, without meaningful changes to user experience. Bitcoin wallet clients could even encourage this migration passively, by paying user change outputs to DASK-supported addresses instead of to pre-quantum BIP32 addresses, and by generating new receive addresses using DASK instead of BIP32. Wallets would be free to migrate coins well ahead of DASK activation. If the DASK consensus changes are never activated, users would not be in any worse position than they were before migrating to DASK.

DASK could also be applied to other post-quantum algorithms besides hash-based cryptography. For instance, an EC secret key could be derived from the hash of a CRYSTALS public key (lattice cryptography). could even be the merkle tree root of some set of public keys from completely different algorithms.

For even better flexibility, the network might treat the hash-based pubkey as a certification key, using a one-time signature algorithm with short signatures which we already know to be secure, such as WOTS. When Q-Day comes, the OTS key can be used to certify a new public key of some yet-to-be-defined algorithm which the community can finalize at the time of DASK activation.

After all, it seems probable that we will have access to more efficient post-quantum signing algorithms on Q-Day than we do today, and WOTS signatures are a relatively small, secure, future proof, and simple way to endorse some undefined future pubkey we don’t know how to derive yet. This certification idea mirrors the SPHINCS framework’s approach of using WOTS keys to endorse child keys without needing to know (rederive) the child keys, so there is at least some well-documented research on this use case of HBS.

Drawbacks

Consensus Complexity. Some ingenuity and compromises might be needed to activate DASK as a soft fork rather than as a hard fork. It seems like transactions mined after DASK which include hash-based signatures would be rejected by older Bitcoin nodes, which expect only an EC signature to claim the same output. I’m not sure whether this is even possible and would love to hear suggestions as to what a DASK soft fork might look like.

Performance. A DASK-supported EC key might take more computational work to derive than an equivalent child key derived via BIP32, because hash-based signing algorithms generally require a lot of hashing to generate public keys, especially WOTS, which pays for its small signature size with worse runtime complexity.

More investigation and empirical benchmarking would be needed to make hard performance claims here. It seems to me at least that any reasonably small trade-off in key-derivation performance would be a price worth paying for quantum resistance.

HD wallets. There is one notable and certain drawback to DASK though: Without unhardened BIP32, extended public keys (xpubs) will no longer be a thing.

We will be forced to drop BIP32 before Q-Day, because existing wallet software treats BIP32 xpubs as safe to distribute. For example, hardware and multisig wallets surrender them frequently as part of normal UX paths. As discussed earlier, when a QA learns a user’s xpub, they can invert it and then derive all child secret keys. Deriving HBS keys with BIP32 would be counterproductive; a defensive wall built atop quicksand.

Instead we would need a new hierarchical-deterministic wallet standard which uses only cryptographic primitives known to be quantum-secure. Currently the only option I know of would be to hash the secret seed, which obviously cannot be shared publicly.

This could negatively affect various use cases in the Bitcoin ecosystem which frequently depend on the ability to independently derive public keys for wallets which a machine might not know the raw private keys for.

  • Watch-only wallets
  • Hardware wallets and other airgapped signing devices
  • Multisignature wallets

However, this is neither a surprising nor insurmountable problem. Other post-quantum solutions share this issue, and further research will be needed to optimize UX or to build an alternative way to non-interactively derive child addresses from public data.

Conclusion

This deep dive into hash-based cryptography has been an incredible horizon-broadening experience for me. Previously, I saw post-quantum cryptography as a dark art, foreign to my understanding, but upon inspection I found the base premises to be elegant and simple. Hopefully this article has demonstrated that post-quantum cryptography need not be magic. We can use systems we already rely on today, in new and inventive ways, to (we hope) defeat future quantum adversaries.

I’m incredibly grateful to the numerous researchers who have poured thousands of hours into inventing, proving, attacking, and standardizing the HBS algorithms I’ve explored in this article. Check out some of the papers linked in this post, and you will see for yourself the creativity and ingenuity which has gone into their designs.

This post has been weeks in the making and yet still there are numerous ideas I have left out. For instance, I may have discovered an optimization to the Winternitz OTS scheme, which might further reduce its signature size, but to give myself enough time to investigate this properly demands I leave it for another day.

I have also neglected other sectors of post-quantum cryptography like Lattice cryptography, STARKS, and many more. The exciting promises they offer and the worrying trade-offs they demand require greater attention than I can afford them in this post. For further reading in this broad domain, check out the Wikipedia article on post-quantum cryptography.

More Resources