How to Bring Your Own Key to a FROST Signing Group

Someone posted this great question on Nostr the other day:

Does FROST allow you to BYOK (make that meme for bring your own key)?

…And being the nerd I am, I couldn’t resist the challenge of working out how to actually do it.

Prerequisites

This article will assume quite a bit of background knowledge.

If you’re not already familiar with elliptic curve cryptography, this article is not for you. Check out my ECC resources page for more beginner-friendly guides.

I’ll assume you’re familiar with the polynomial-driven mathematics which underlies Shamir Secret Sharing, as FROST relies on very closely related principles.

Background

FROST is a threshold multisig protocol which allows a group of mutually distrusting parties to co-sign a message in unison, producing an aggregated Schnorr signature. This signature can be validated using a single public key which is controlled collectively by the whole group, so third-party verifiers don’t need to care how the signatures are produced - only that they are valid Schnorr signatures.

Sounds a lot like MuSig, right? Well, in MuSig, all signers in the group must be online to sign a message (-of-). A FROST group on the other hand can set an arbitrarily low security threshold, commonly denoted as . This threshold determines how many signers must be online and cooperating to sign a message (-of-). This is helpful in situations where some signers might not be online or cooperative all the time, but a single unified signing key is still needed.

The FROST protocol is split into two sub-protocols:

1. The distributed key generation (or “DKG”) protocol
2. The signing protocol

The DKG protocol sets up the signing group so that each party receives a fairly-computed and verifiable signing share. The signing protocol utilizes at least of those signing shares to construct a signature.

For this article, we won’t look to hard at the signing protocol. We really only need to care about the DKG, and whether it outputs secure signing shares in different use cases.

Notation

Just so we’re all on the same page:

Notation	Meaning
	The base-point of the secp256k1 curve.
	The SHA-256 hash function.
	The order of the secp256k1 curve. There are possible valid non-zero points on the curve, plus the ‘infinity’ point (AKA zero).
	Sampling randomly from the set of integers modulo . Note that we exclude zero when sampling.
	Define the set of all for every number in the range from to .
	Inclusive range notation, i.e. all numbers between and including and .
	The union of sets and .

DKG Review

This section is mostly a review of Section 5.1 Figure 1 in the FROST whitepaper. Feel free to skip ahead to the new stuff if you're already familiar with FROST.

The canonical FROST DKG protocol (also known as a Pedersen DKG) starts with each of the prospective signing group members generating random coefficients. Each uses these coefficients to define a degree polynomial.

• denotes the index of the signer, which should never be zero.
• denotes coefficient indexes starting from zero.
• Each denotes the random coefficient at index chosen by signer .
• is the polynomial defined by these coefficients.

Each signer then computes a commitment polynomial , which is essentially a public version of their secret keygen polynomial .

Each signer computes a proof that they know - the constant term of . This prevents rogue key attacks. In simpler terms, they sign a message to confirm they know their secret coefficient .

• is a random nonce.
• is a context string unique to this DKG execution, which prevents replay attacks.
• is the resulting proof - AKA signature - which demonstrates the signer knows .

Each signer publishes the proof and the commitment polynomial to their fellow co-signers. Signers wait to receive all commitment polynomials and verify all proofs before continuing. These proofs can be validated quite easily by checking the signature against the pubkey , in exactly the same manner as verifying a normal Schnorr signature.

Once all proofs have been verified, and all commitment polynomials are available and consistent across the group, each signer computes evaluations using their secret keygen polynomial , for every signer index in the group. Each evaluation is sent to only the one signer.

For instance, signer would compute and give that evaluation only to signer . Repeat for every signer in the group, including one evaluation which they keep to themselves:

If there are signers in the group, then each signer receives evaluations of different polynomials, all of which should have the same degree (), but totally unrelated random coefficients.

Each evaluation must then be verified. Every signer has the full set of commitment polynomials, . Each polynomial commitment can be used to verify the evaluation given by its original sender.

Let’s say we’re signer , and we received an evaluation from signer . This evaluation should be . We can verify it easily using to assert the following statement.

If that holds, then we know the evaluation we received from signer is authentic, or at least consistent with their commitment polynomial.

If it holds for every evaluation received from all signers (including themselves), then signer can at long last compute their final FROST signing share by summing up these evaluations.

The FROST group also has a public verification polynomial , which can be computed by any signer as:

• outputs the FROST public verification share for signer .
• outputs the FROST group’s collective public key.

The DKG succeeds if all signers correctly verified their new signing shares, and can all agree on the same verification polynomial .

What’s Going On Here?

This has a surprising result.

Every FROST signer in the group ends up with a Shamir Secret Share of a hypothetical commonly-generated secret . None of the signers ever learned . If at least one signer chose their constant term randomly, then is totally random.

Here’s an analogy for you. Every signer rolls a die and puts their die in a hat. The shared secret is the sum of all those dice, mod 6. If even one player rolls their die fairly, then it’s impossible to guess what that shared secret is with any better than a chance. Also the hat is protected by a magical spell so that you can’t look inside it without at least of the signers cooperating. Yeah, cryptography is magic.

FROST keygen is kind of like Shamir Secret Sharing, except where the group’s shared secret is constructed randomly, and collectively, instead of by a trusted dealer.

How did Shamir Secret Sharing sneak in there? Well FROST signing shares are exactly the same mathematical objects as Shamir Secret Shares. Each signing share is an input/output tuple , where is the evaluation of some hypothetical key-generating polynomial , whose constant term is i.e. the group’s collective secret key. If or more signers were to cooperate, they could use Shamir Secret Sharing to reconstitute the group secret key .

This works because the group’s collective keygen polynomial is defined by adding up all the individual secret keygen polynomials chosen by the signers.

Summing two polynomials is just a matter of adding their terms together. Graphically, this feels like adding up the distance from the X-axis between the graphs of both functions.

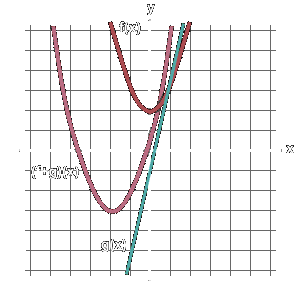
By adding up the evaluations they received , the signer is composing an evaluation (AKA a share) of .

The only difference between SSS and FROST is that FROST provides an interactive signing protocol to sign messages without reconstituting (which is the really novel part of FROST). Fundamentally, any SSS group is also a FROST group, and could sign messages as a group if they so chose.

---

Now that we understand how FROST’s DKG works within its intended domain of usage, let’s examine how we might modify it to support Bring-Your-Own-Key (BYOK). In pursuit of such lofty goals, we’re going to be bending FROST’s DKG in ways it wasn’t intended. With that in mind, here’s a big fat disclaimer.

Hypothetical Crypto Ahead ⚠️

Everything you’re about to read below is completely hypothetical cryptography which I completely made up myself. Nobody has peer reviewed this. Nobody has audited this. As far as I know, there is no precedent for the operations I’m doing here (If there is, please let me know!). I’m not a PhD-bearing expert. Even if I were, you shouldn’t implement cryptography you read about on some guy’s blog. I’m writing this to spur discussion and to theorize, not as reference material for production-grade crypto. Stick to battle-tested and peer-reviewed protocols.

BYOK

To BYOK, some subset of the signers must enter the FROST group with a-priori fixed signing and verification shares. The role of the DKG then, is to compute signing and verification shares for the other non-BYOK signers, and also to verify each other’s shares are valid.

Limitations

One corollary of the Fundamental Theorem of Algebra is that any points can only be interpolated by a polynomial of degree or higher. We can use this to put an upper bound on .

The group keygen polynomial must interpolate (pass through) every signing share . If of those shares are fixed at arbitrary values before the DKG protocol is executed, then must have degree at least .

In practice, this simply means no more than signers can BYOK to a FROST group with threshold .

Flipping the DKG

Let denote an a-priori fixed secret signing share, brought by one of these signers to the DKG. They must keep secret, otherwise it has no value.

Without loss of generality, I’ll assume that signers are the BYOK signers, and signers are the standard FROST signers who are OK with generating fresh keys.

We need a way to guarantee that specifically for the set of signers who BYOK, but not necessarily for the other standard FROST signers. We also can’t compromise the security of the DKG by doing this.

The FROST DKG assumes each signer generates their keygen polynomial by choosing random coefficients and then using them to produce evaluations, but they can do just as well starting the other way around: by going from evaluations to coefficients.

The most obvious way to do this is to have every signer design their keygen polynomial so that it outputs specifically at all BYOK indexes . Each BYOK signer can adjust their keygen polynomial to output . The result is that , because all the other evaluations cancel out.

This sounds challenging, but it’s actually relatively easy to design polynomials in this way, by using methods like Lagrange Interpolation, and none of this requires a-priori knowledge of the public keys being brought to the group (meaning we should still be safe against rogue key attacks).

Interpolating

Assume we have some black box interpolation algorithm which takes in some set of points called , and spits out a unique polynomial which has degree at most .

Each FROST signer first samples a set of random evaluations which together constitute their contribution to the group keygen polynomial.

They can compute their individual keygen polynomial by interpolating those points, plus the zero-evaluations at indexes needed to enable BYOK.

• is the set of evaluations chosen by the signer which contribute to the randomness of
• is the set of zero evaluations which enable BYOK for some signers.
• is the union (that’s the operator) of and
• is an interpolation mechanism which spits out our signer’s desired keygen polynomial

For a signer who is bringing their own fixed key, they simply amend to include the appropriate evaluation output .

Other differences from the standard DKG process:

1. Each signer constructs their keygen polynomial by interpolating a set of points in total. This is to ensure (and by extension, ) will have degree , but it also has an interesting security implication. If (the threshold is the same as the number of signers who BYOK), then is an empty set. This implies that a group of signers who BYOK are entirely determining everyone’s keygen polynomials, and thus also determining the final group keygen polynomial .

This sounds pretty bad. Couldn’t those BYOK signers collude to poison the group key? Well if , then those same BYOK signers could run off with the whole key even if we used the standard FROST DKG anyway. No new opportunities there.

2. When sending evaluations, signers can skip the BYOK indexes , because those have already been fixed ahead of time.

Other than this, the protocol runs exactly the same as the standard FROST DKG.

• Commitment polynomials are still
• The knowledge-of-secret-key signature is still required and must be verified.
• Evaluations must still be sent to those who did not BYOK.
• Individual signing shares (which are not BYOK) are still computed as
• The group verification polynomial is still constructed by summing all commitment polynomials.
• The group’s public key is still computed as .

The math works out correctly. The big question is whether this is secure or not.

Security

The main approach I considered when trying to attack this protocol was whether a colluding subset of BYOKers could somehow backdoor the group key. Although they are able to reduce the overall entropy involved in the DKG process (because only of the evaluations used to interpolate is random), I am unsure how that could be exploited. Even if their entropy is decreased, the group key and signing shares produced by the DKG are still randomly distributed, and so they should be secure (?).

Far be it from me to authoritatively declare whether this approach is secure or not. Intuitively it feels secure, because I can’t think of a way to attack it effectively with less than signers.

But this is not a solid metric. These days, cryptographic security is best when it can be proven definitively under clear assumptions. I would love if those more experienced than myself could inspect this idea and possibly prove whether the approach is secure.

Use Cases

If FROST BYOK is secure, what can you do with it? Well there’s one thing it might be very handy for.

BYOK would allow us to build hierarchical FROST groups from the bottom-up, in the same way we can currently do with MuSig key aggregation. A hierarchical FROST group is one where signing shares are themselves split among a threshold of “sub-signers”. For example, this diagram illustrates a 2-of-3 multisig with nested subwallets, each of them a FROST wallet.

                            ┌───────────────────┐
                            │                   │
                            │ wallet A (2-of-3) │
                            │                   │
                            └─────────┬─────────┘
                                      │
                                      │
            ┌─────────────────────────┼───────────────────────────────┐
            │                         │                               │
            │                         │                               │
            │                         │                               │
┌───────────┴──────────┐  ┌───────────┴──────────┐         ┌──────────┴───────────┐
│                      │  │                      │         │                      │
│ subwallet 1 (1-of-2) │  │ subwallet 2 (1-of-2) │         │ subwallet 3 (2-of-3) │
│                      │  │                      │         │                      │
└──────────┬───────────┘  └───────────┬──────────┘         └──────────┬───────────┘
           │                          │                               │
     ┌─────┴──────┐             ┌─────┴──────┐           ┌────────────┼────────────┐
     │            │             │            │           │            │            │
┌────┴────┐  ┌────┴────┐   ┌────┴────┐  ┌────┴────┐ ┌────┴────┐  ┌────┴────┐  ┌────┴────┐
│signer 1A│  │signer 1B│   │signer 2A│  │signer 2B│ │signer 3A│  │signer 3B│  │signer 3C│
└─────────┘  └─────────┘   └─────────┘  └─────────┘ └─────────┘  └─────────┘  └─────────┘
     X                                                   X            X

If each of the signers marked with an X agreed to sign some data, then in theory they could trustlessly sign as the top-level wallet A. Signer 1A can sign as subwallet 1, while signers 3A and 3B can sign as subwallet 3.

This is not anything new: Normal FROST signing shares from the DKG can be split into Shamir Secret Shares and distributed to new keyholders to form such a hierarchy. The signing protocol becomes more complicated, but it’s completely doable. However, with standard FROST, participants must always generate a completely fresh signing share when creating a new FROST group. Pre-existing FROST groups cannot join together trustlessly into a higher-order FROST hierarchy without abandoning their existing group keys.

What’s novel about this approach I described above is that BYOKing allows existing FROST or MuSig group keys to be composed into hierarchical FROST groups, albeit with an upper limit on the number of allowed BYOKs ().

As to how this could be used in the real-world, I’m not sure. Perhaps BYOK could enable things like higher-order Fedimints, to enable composing multiple Fedimint instances together into a SuperMint™.

Contact

Hit me up via email, or on Nostr to chime in on this subject! You’re also welcome to file a pull request or issue for this website if you notice any mistakes or would like to add something.