Issuing New Shamir Secret Shares Using Multi-Party Computation

cryptography

Shamir’s Secret Sharing (SSS) is a well known tool in the cryptography community. It is used in protocols like SLIP39 and FROST. SSS is popular because of its property of information-theoretic security (it is secure even against adversaries who have infinite computational power).

SSS is a powerful cryptographic tool, but it struggles in terms of flexibility. If a share is lost, it is not easy to issue new ones. Adding new shares is possible if enough shares are brought together to recover the original secret, but what if shareholders do not wish to reveal their shares to each other yet? What if they never want to reveal their secret shares, as would be the case with a threshold multisignature protocol such as FROST?

What if the shareholders distrust each other, or the dealer? How can they be sure their shares, or the shares of others, are valid?

In this article, I’ll cover the basics of how Shamir’s Secret Sharing works. I’ll demonstrate how to extend it with verifiable properties so that the dealer and shareholders need not trust one another. Finally I’ll describe a procedure which can be used to trustlessly issue new shares without recovering the full original secret. All the while, shareholders don’t need to trust each other or the dealer, and learn nothing about the new share they issued.

Notation

Just so we’re all on the same page:

Notation Meaning
is a member of set .
The set of integers mod .
Sampling randomly from the set .
A deterministic concatenation of and .

Polynomials

The basis of Shamir’s Secret Sharing lies in the fundamental theorem of algebra, specifically in the mechanics of polynomials, so we should do some review of this domain before we dive into SSS.

Review

  • A polynomial expression is any expression of variables* that involves only addition/subtraction, multiplication/division, and positive-integer exponentiation.
    • Usually single-variable polynomials denote the variable as .
  • The degree of a polynomial is the highest power of the variable used in the expression (with a non-zero coefficient).
  • The coefficients of a polynomial are the multipliers alongside each power of the variable when it is in standard form.
  • The roots of a polynomial expression are the values of which cause the expression to evaluate to zero.
    • Sometimes the roots of a polynomial are complex, meaning they involve numbers which make use of the imaginary number . Don’t worry, we won’t be dealing with complex numbers today!
  • A polynomial function is a function which can be computed by simply evaluating a polynomial on an input .

* Note that today I’ll be writing exclusively about univariate (single-variable) polynomials, where the variable is denoted .

For example, is a polynomial function with degree (AKA a cubic polynomial). Its coefficients are for the cubic () term, for the linear () term, and for the constant () term.

Polynomials aren’t only written in standard form though. They could be written in factored form, such as , or a mix of the two, like . As long as only the addition/subtraction multiplication/division and natural number exponentiation operations are used on the variable , it is still called a polynomial.

By contrast, a function like is not a polynomial because it takes the base to the power of . Such a function doesn’t behave according to the laws of polynomials.

Almost everyone will have at least some experience handling polynomials, as most high school math classes deal extensively in linear (degree ) polynomials such as , and quadratic (degree ) polynomials such as . Students are taught how to factor them, expand them, find their roots, graph them, and many other things, but only in university level mathematics would you be taught how powerful these tools are for cryptography.

Interpolation

The Fundamental Theorem of Algebra states:

Every non-zero, single-variable, degree polynomial with complex coefficients has exactly complex roots.

In other words: If a polynomial has degree , then there are exactly different values of which make it evaluate to zero (if we include complex numbers). If you think about the shapes that these functions take on the Cartesian Plane, this makes sense.

This theorem has a helpful consequence.

Say we have a set of points , where all values are distinct (i.e. ). Then there exists some unique polynomial function of degree at most which passes through all points, such that for each point from . A common way to phrase this is that interpolates the points .

Uniqueness: Proof by contradiction

How do we know is unique? We will assume it isn’t true. In exploring the consequences of that assumption, we will find a logical contradiction.

Assume there exists two non-zero polynomial functions and of degree at most which pass through those points, such that for at least one input (indicating the polynomials are different), but also that for all points.

Since and each have degree at most , each has at most roots.

Consider the difference between the two polynomials . Since we assumed , this implies .

Since at all , it follows that for all as well. This implies the polynomial has at least roots.

Recall was defined as , so can’t have a higher degree than either or , which we assumed have degree at most . Adding and subtracting polynomials merely adds or subtracts their coefficients without introducing higher-degree terms. Thus must have at most degree .

This is a contradiction. On one hand, must have roots. On the other hand, it must have degree at most , which - due to the Fundamental Theorem of Algebra - means it must have roots.

This contradiction is proof that must be equal to the zero polynomial (i.e. ). This is the only logically consistent way for to have roots while also having degree at most .

The very special and helpful property of interpolating polynomials is: To interpolate a polynomial of degree , we need at least evaluations of (i.e. points that passes through).

Said differently, if we create evaluations of , such as , then only of those evaluations are needed to reconstitute and thus evaluate it at any input. With any fewer than evaluations, we would gain no new information about itself, because there exists an infinite number of degree polynomials which pass through those same or fewer points.

Perhaps by now you might be starting to see why polynomial interpolation is at the heart of Shamir’s Secret Sharing.

Demonstration

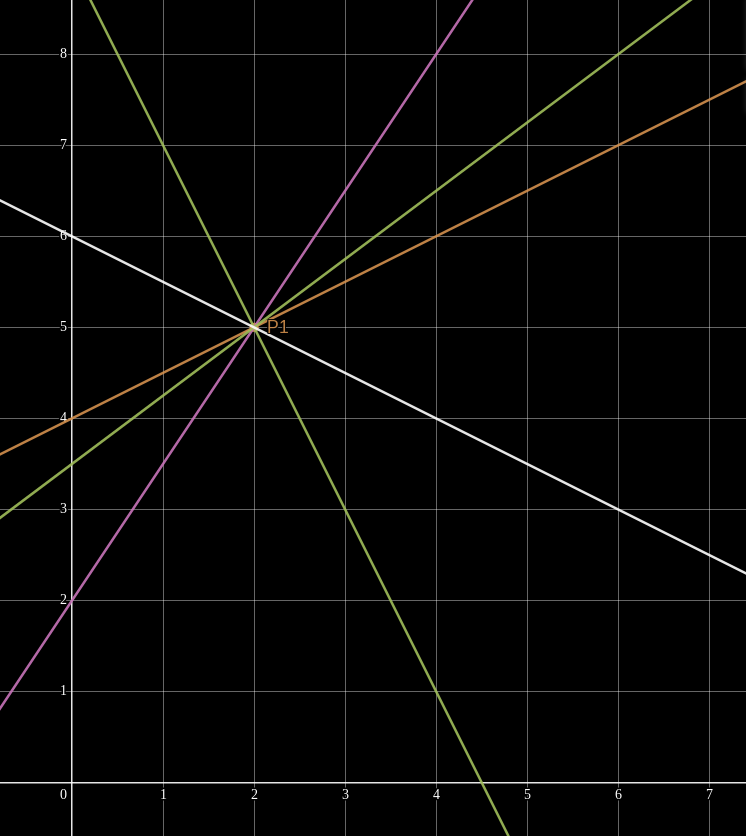
This concept is easier to understand visually with linear polynomials. Picture two points and on the Cartesian plane.

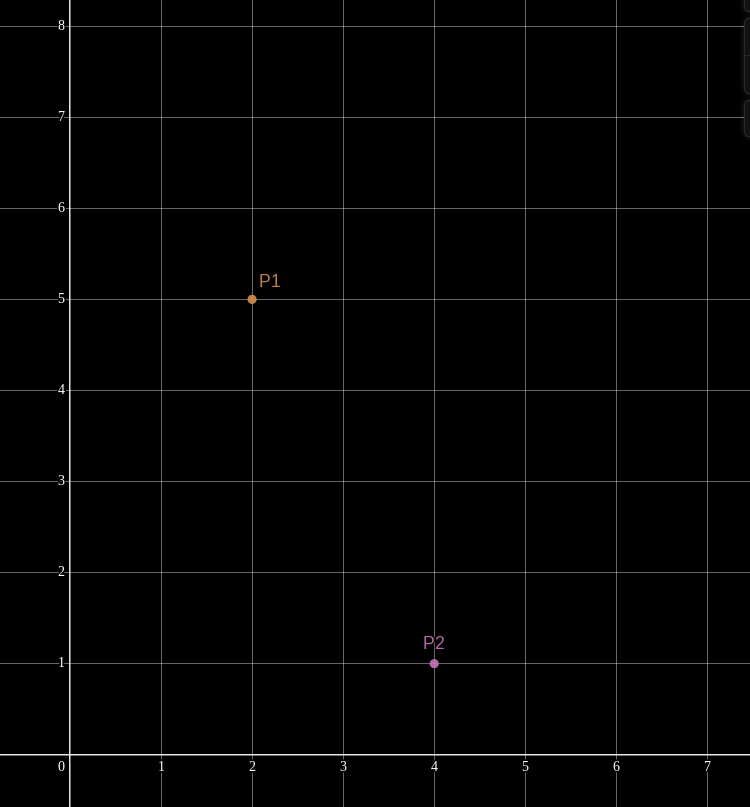
Any two points are sufficient to uniquely describe a line between them. Remember that a line on the Cartesian plane is just a degree-1 (AKA linear) polynomial. Only one unique line (polynomial) passes through (interpolates) the two points.

In this case, the polynomial happens to be .

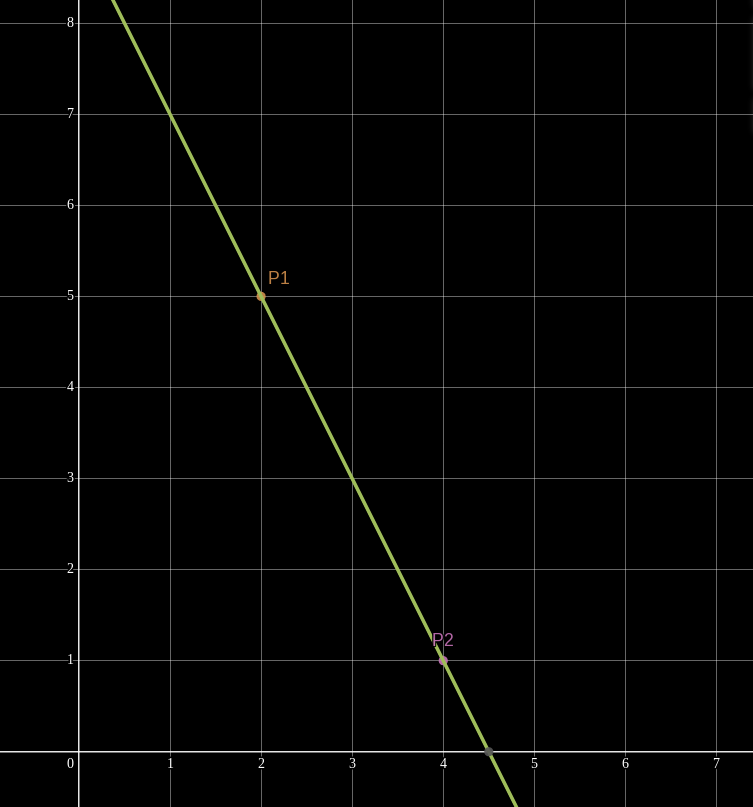
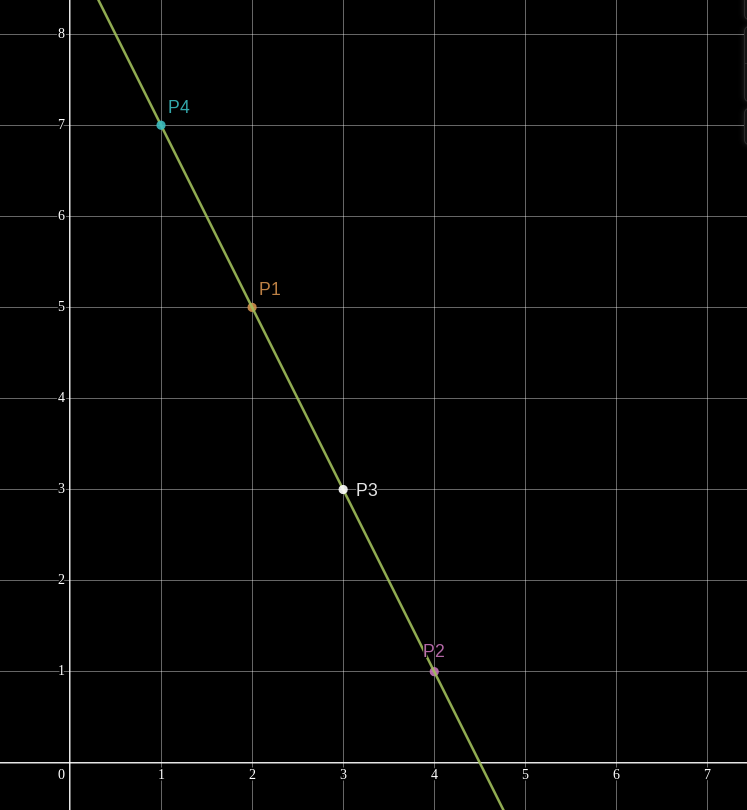
If we are given additional points and located along the same line, this doesn’t change the polynomial function which interpolates all four points.

However, if we are given only one evaluation, say where , we gain no information about because there are infinite other linear polynomials (lines) which pass through the same point.

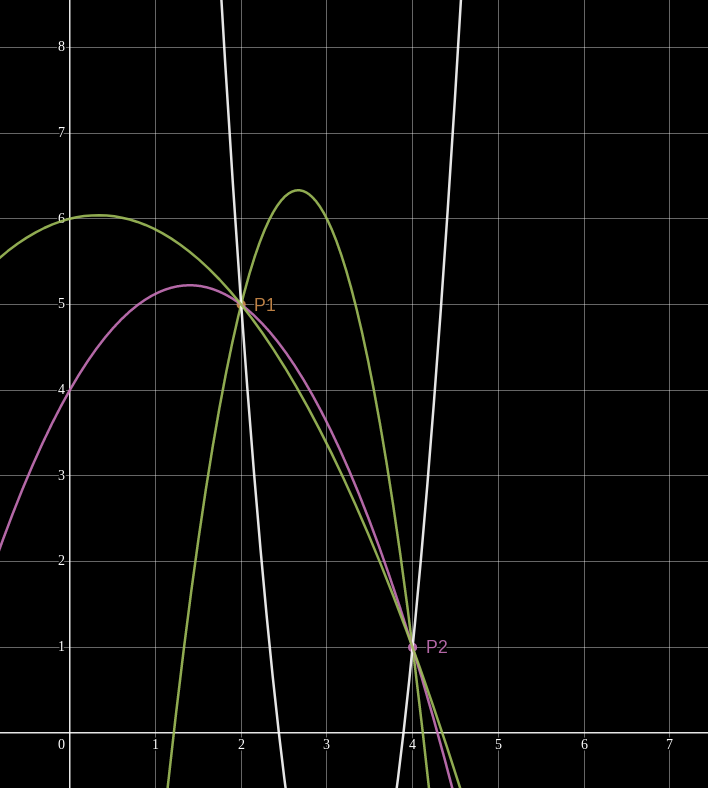
This concept generalizes to higher-degree polynomials! Given the same two points and , there are infinite degree-2 (AKA quadratic) polynomials which pass through those points.

But add a third point and suddenly we can find only one quadratic polynomial which interpolates them.

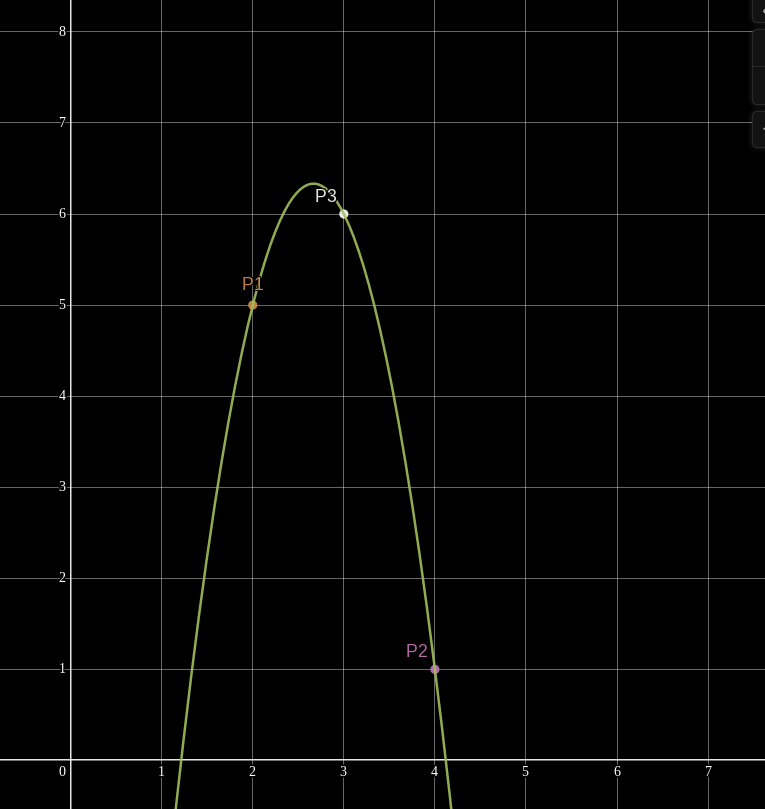
but how would we actually do the interpolation?

There are many ways to skin this cat. Given data points, the polynomial we interpolate from them would be the same. As long as our method works and works quickly, the mechanics aren’t crucial to know at this point. Many interpolation methods exist:

  • Lagrange Interpolation (the most commonly known)
  • Newton Interpolation
  • Inverting the Vandermonde Matrix (uses linear algebra)

For the time being, assume we have some black box interpolation algorithm which takes in some set of points called , and spits out a polynomial which has degree at most . I’ll discuss how works a bit later. By now you’re probably dying to know how this all applies to Shamir’s Secret Sharing.

Shamir’s Scheme

This wouldn’t be a math article if we don’t start by defining some parameters.

  • Let be a Finite Field containing elements, where is some large prime number.
    • If you’re not familiar with Finite Fields, just consider it as a special group of numbers, such that addition, subtraction, multiplication, and division all work normally as they do within the real numbers, except there are a finite quantity of possible discrete numbers that can be used.
    • Usually, this is the set of integers modulo a prime number , AKA .
  • Let be a secret such that . Our goal is to break into shares so we can distribute them.
    • Usually is just some large random number randomly sampled from , such as a private key.
  • Let be the total number of shares we want to issue.
  • Let be the minimum number of shares required to reconstruct , such that .

Distribution

Shamir’s Secret Sharing scheme starts with a trusted* dealer who knows and wants to distribute it evenly as shares, such that any subset of at least shares can be recombined to recover . For example, the trusted dealer might be backing up a signing key or encryption key across physically distributed locations, or with trusted representatives such as staff, attorneys, family, and close friends.

* There are other schemes which allow mutually distrustful parties to generate shares of a common but yet-unknown secret, but that is out of scope for today.

  1. The dealer samples random values from .

  2. The dealer treats as the coefficients of a degree polynomial function .

  1. The dealer assigns each share a unique index , labeling each share . They could be randomly selected, but usually indexes are just the ascending natural numbers, so we’d have . The indexes must not be zero and must not have repetitions.

  2. The dealer evaluates at each of the different indexes.

  1. The dealer distributes shares as tuples of . is the private data within each share which must be kept secret.

Recovery

At recovery time, the original secret is assumed to no longer be available - Perhaps it was lost in a boating accident, or left encrypted with an unknown password. Perhaps the original dealer was hit by a bus and her representatives are now charged with handling her affairs. Perhaps the dealer is no longer willing to cooperate. Regardless, the shareholders must recover independently, using only their shares.

Let be the set of or more share indexes which are participating in the recovery. We assume that at least shares are available. Some shareholders might not be online or might also have been hit by aforementioned bus. Some shares may have been physically destroyed, such as in house fires or boating accidents. As long as shares are still available, and can be reconstructed.

Each of the shares in is given to some trusted* recoverer whose duty is to reconstitute the original secret given or more shares. The recoverer might be one of the shareholders, or an independent entity.

* Care is needed here. If the recoverer is malicious, they might use themselves for some nefarious purpose. SSS doesn’t specify what to do once is recovered - It is quite limited in that capacity. Canonically, SSS is solely a secret backup and recovery tool. What comes after is up to the implementation.

  1. The recoverer is given a set of or more shares . Shares must have unique indexes.

  2. The recoverer treats the shares as the evaluations produced by some degree polynomial function over , such that for all .

  3. The recoverer uses a polynomial interpolation algorithm to interpolate the polynomial .

  4. The recoverer evaluates . This outputs , because:

Gotchas

SSS seems simple, but it is an easy protocol to screw up in practice.

  • It is very important that the non-constant coefficients of are totally random, otherwise the information-theoretic security of SSS is lost.
  • When distributing shares, it is crucial that the dealer does not distribute a share evaluated at index zero, because since , they would be giving away the secret .
  • Shareholders must be trusted not to use phony shares when recovering. If one shareholder submits a phony or faulty share, they could change the secret which is recovered to something unusable, and nobody would be able to tell which shareholder screwed up.
  • There must be a trusted recoverer machine and a trusted dealer machine who will both know . If either is compromised, will naturally be exposed.
  • The dealer and the recoverer must use the same finite field , which could result in incompatibilities if this field is non-standard.

But still, the power of SSS is undeniable, especially as a primitive when combined with other tools.

Before we demonstrate how shareholders can trustlessly issue new shares, I want to take a moment to learn about how can be interpolated. If you’re already familiar with polynomial interpolation, click here to skip ahead.

Interpolation

In my opinion, the most intuitive interpolation method is Lagrange Interpolation. First discovered in 1779 by Edward Waring, this method is named after the scientist Joseph-Louis Lagrange who made the method famous.

The Lagrange method takes a step-by-step approach to achieve a polynomial with all of our desired qualities. Given points with distinct -coordinates, we should be able to find a polynomial function which:

  1. interpolates all points ()
  2. has degree at most

Where to begin? We can make use of the Fundamental Theorem of Algebra once more: A degree polynomial will have roots - i.e. it outputs zero at different inputs.

Since we are given points, we can define a degree polynomial which outputs zero at all inputs , specifically excluding the input where it outputs… something which is not zero.

This is the simplest polynomial we could define with roots at . If we plug in any , then .

Seems weird to do this, but now has a handy property: Out of all the -coordinates we care about, it only has a non-zero output specifically at . That output can be predicted in advance and scaled however we’d like it.

Specifically, we can scale by multiplying by and dividing by . This scales the output to when we input .

Let’s define this operation as a new polynomial function .

As a result, outputs our desired value at input , or it outputs zero at all other .


We can expand and regroup factors to make everything more readable.

Imagine if we repeat this for all , and we find . Since each passes through the point but outputs zero at all , then the sum of all would be a new polynomial which interpolates all the points .


More commonly, this is written in the mathematical literature in terms of a basis polynomial which outputs at and zero at . Then the output of is scaled by a factor of . The textbook definition of a Lagrange Interpolation Polynomial is usually written as


Notice how only needs in order to be evaluated - its definition doesn’t require any of the -coordinate values, so can be computed on any input by anyone who knows , whether or not they know the corresponding evaluation outputs .

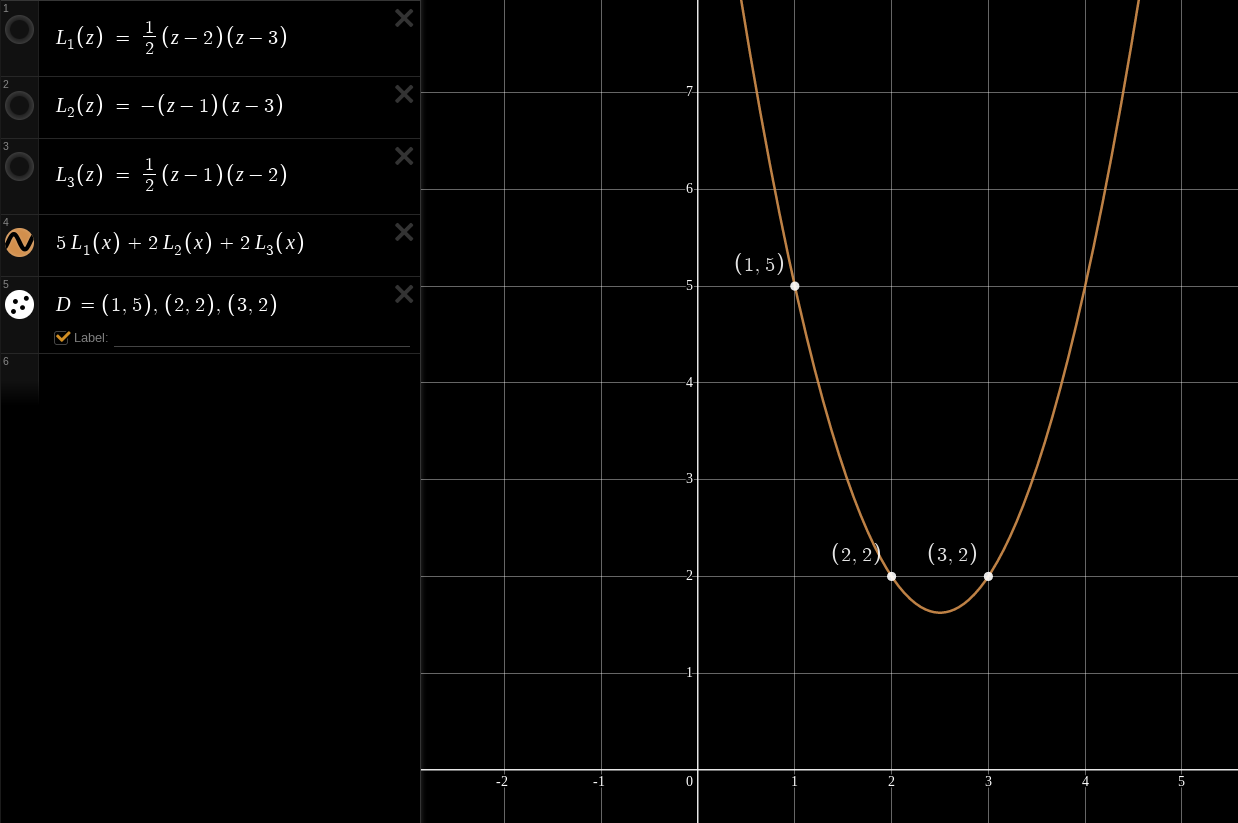
A common way that modern academic papers will represent the basis polynomials is by calling them Lagrange Coefficients defined for some constant . They will usually be given some greek symbol such as (lambda), with the subscript representing the value in the point which is being interpolated by that specific basis polynomial.


Example

Here we explore three basis polynomials for the -coordinates .



Let’s say we are given the -coordinates , so the array of points we want to interpolate would be .

We can compute our interpolated polynomial on any input by evaluating .

This straightforward method is at the heart of numerous clever algorithms, including Shamir’s Secret Sharing.

There are other improvements we could make to speed this procedure up and increase accuracy for floating point arithmetic - Read about the Barycentric Form of Lagrange Polynomials for more.

But for our purposes this is sufficient background knowledge to proceed to the next section. What I really want you, dear reader, to remember, is how the basis polynomials are constructed. In particular:

  • We can give any polynomial a root at any constant by multiplying a polynomial by .
  • When we add two polynomials and together, the roots of either function take the value of its counterpart instead. If , then is the same as .

We will make use of these properties in the next section.

Trustless Sharing

Not so well-known as Shamir’s scheme is Feldman’s Verifiable Secret Sharing (VSS) scheme. This variant of Shamir’s scheme allows participants who distrust each other or the dealer to verify shares are evaluations for a given secret. This turns out to be a very useful property for trustless protocols like multisig.

For Feldman’s VSS, we must introduce a group generator . For this article, I’ll be using an elliptic curve generator point with order , so our finite field will be set to the integers mod , i.e. . Check out these elliptic curve cryptography resources to learn more about how elliptic curves work.

In principle, this works for any kind of discrete-log group, including multiplicative groups of integers modulo any prime number , but the notation is easier to understand using an additive group like an elliptic curve.

Distribution

For Feldman’s VSS extension, the dealing phase of SSS is modified as follows.

  1. After computing the coefficients , the dealer computes a set of commitments to the secret and every other coefficient , such that


Notice that is the discrete logarithm (secret key) of . In a way we could think of as the public key for , which might prove useful to the verifying shareholders, depending on the context of the implementation.

  1. While distributing the shares, the dealer broadcasts to all shareholders, in such a way that shareholders can be sure they all received the same commitment from the dealer. If no secure broadcasting message system is available, the shareholders must compare with one-another independently to verify they all hold the same values of .

  2. Each shareholder can verify their share is valid under by testing that . This works because act like public equivalents of the secret coefficients which define the dealer’s polynomial .

Knowing doesn’t give the shareholders any secret information about , assuming is not computable (i.e. assuming the elliptic curve discrete log problem is hard). But does give shareholders the ability to verify shares are valid for a particular polynomial commitment .

This way, shareholders don’t need to trust the dealer to distribute shares fairly. Perhaps the dealer might be unfair, or faulty. This gives shareholders a way to confirm with each other that they all hold shares of a secret, and that with at least shares they can recover the secret key of .

Recovery

This verification can also be done at recovery time by the recoverer. The recovery process can be modified as follows:

  1. When receiving shares, each share is sent as where is the original commitment as known to the bearer of share .

  2. Each share is verified against during recovery. All reported commitments must be the same ( holds for any and ).

Any minority of shareholders who submit mismatching commitments or invalid shares can be detected. If all shareholders in behave, then and only then can recovery succeed.

Shares as Keys

If we treat each share as a secret key, then knowledge of gives each shareholder the ability to compute the “public-key” of any other share .

This gives each shareholder a way to prove they own a given share without revealing it: Just sign a message with the secret key . Anyone who knows and can verify the message by computing the public key and verifying signatures against it. Similarly, any could be used as an encryption key to exchange messages which only specific shareholders can read.

Issuing a New Share

Suppose a dealer has issued Shamir shares and has disappeared, or has deleted the secret and the coefficients . In such a situation, the only way to recover the secret is with or more shares.

Suppose that a quorum of shareholders possessing at least shares wish to issue a new share (or recover an existing one) at index , and distribute it to a new (or existing) shareholder. There are many reasons this might be needed:

  • A existing share was lost in a boating accident.
  • A existing shareholder was hit by a bus and nobody can find her share.
  • A new shareholder is to be inducted into the group.

The naive method would be to bring those shares together on a trusted recovery machine, and interpolate the original polynomial constructed by the dealer. The recoverer could evaluate on any index at which the new share should be issued. That share could then be transmitted (securely) to the new shareholder as . Effectively, this is like performing the recovery stage followed by a half-way execution of the dealing stage under Shamir’s original scheme.

However this comes with a major drawback: There must be a trusted recoverer who reconstructs the full polynomial in-the-clear in order to issue a new share. This implies reconstructing as well. The new share could be exposed: first in the very process of its computation, and again when it is forwarded to the new shareholder.

Ideally, shareholders should be able to issue new shares without reconstructing on a single, potentially vulnerable machine, using some interactive multi-party computation, in a way that only the recipient of the new share can learn it.

Disclaimer

Don’t implement this in a production environment!

Although I believe I have effectively proven the security of this protocol below, there may be some loophole which would allow a malicious shareholder to learn more about or the secret . I would much appreciate extra review on this concept and feedback about whether its security reduces to other proven schemes.

The Mission

There is a set of shareholders who want to issue a new share, or recover an existing one, at index , but none of them want to expose their secret shares to one-another yet. Similarly, the new shareholder is also timid, and would prefer if only they learn the new share and nobody else.

Let represent the set of share indexes which are participating in the issuance protocol.

Each bearer of share knows . Each shareholder knows their own index . To construct a new share at index , shareholders in wish to give an evaluation of to shareholder without learning themselves.

Assumptions

For simplicity I may write as though each share at index is held by one shareholder - a person or a machine - but the same protocol works if some shareholders hold multiple shares.

It is crucial that each shareholder of can communicate with one-another over a secure and identifiable channel. Shareholders of can also all communicate securely with the new shareholder at index .

Strategy

In this section I’ll describe the strategy we’ll use to attack this problem at a high level, and hopefully motivate the concept.

Consider a blinding polynomial (that symbol is a beta) of degree , constructed by random sampling from . This polynomial outputs apparently random nonsense at all inputs, except input at which it outputs zero.

Now consider the issue polynomial (that symbol is a zeta) for , which is the sum of the original share-creation polynomial and the blinding polynomial .

inherits the the interesting property from the blinding polynomial where it outputs random nonsense at every input except . Since and is just the desired share , it follows that also outputs the desired new share , but at any other input is meaningless nonsense - it is blinded at all other inputs.


Our strategy will be for participants in to jointly evaluate the issuance polynomial at different inputs, and then pass those evaluations to the new shareholder for index . The new shareholder can interpolate and compute to get their share of the secret. Since ’s output is otherwise random, no additional information is learned by interpolating the polynomial - that is, unless someone can somehow interpolate and subtract it from .

Participants in must not learn or more evaluations of - otherwise they would also learn . They must each contribute to the evaluations, otherwise the ritual might be rigged by some subgroup of malicious shareholders.

The question then becomes: How can the issuers in construct and evaluate fairly and without exposing secret data to each other?

Multi-Party Computation

All shareholders in must work together to build . If is constructed by a single shareholder or by a cabal of corrupted shareholders, they could collude with the new shareholder to learn and run off with the secret .

We can use multi-party computation practices to construct a joint polynomial which all shareholders in contribute to.

Each shareholder constructs a random degree polynomial, and multiplies it by to produce a degree polynomial which has a root at . This polynomial is then denoted - the partial blinding polynomial for share . We will then define the joint blinding polynomial as the sum of all partial blinding polynomials for all .

This ensures that the joint blinding polynomial will be random as long as at least one shareholder is honest. Imagine all shareholders pouring a bit of paint into a central glass. Even if shareholders were to pour water into the cup, as long as at least one shareholder pours a real paint, the color of the resulting mixture will not be fully transparent.

Procedure

Beware: The procedure I describe in this section is unverifiable for old and new shareholders alike. Shareholders must trust each other not to attempt denial-of-service or griefing attacks by issuing faulty contributions to the multi-party computation. I’ll discuss how to make this fully trustless in the next section.

  1. Shareholder samples random coefficients and uses them to construct their partial blinding polynomial as follows.


  1. Shareholder computes for every other share , and distributes each to the bearer of share .

  2. Each bearer of share waits to receive all - the evaluations of other polynomials on his index .

  3. Once in possession of all , the shareholder can compute by summing all .

  1. Remember how we defined ? The bearer of share sums and to yield . This is because the share is just the evaluation of , as mentioned earlier.

  1. Each shareholder sends the evaluation to the new shareholder of index , for a total of points .

  2. The new shareholder runs the interpolation algorithm to yield the degree polynomial , which they can compute at to learn their new share .



is just as valid a share as any other. Its bearer is on equal footing with the rest of the shareholding group. They can save and conclude the issuance session by broadcasting a confirmation to the shareholders in .

At this point, each shareholder can safely discard and its coefficients to ensure they don’t fall into the wrong hands.

Caution! could be any index, but it must be agreed upon ahead of time by the whole issuer quorum , as only holds for . For all other inputs, spits out nonsense.

Practically, should be chosen as an index whose share is certain not to be available to anyone, otherwise the issuers might duplicate someone else’s existing share. Maybe Steve didn’t get hit by a bus - maybe he just turned his phone off for a vacation. Upon his return, he’ll be pretty upset that we gave his share to someone else. The group would need to find some way to revoke the duplicate shares (a topic for another day).

Verifiable Procedure

The above protocol works in the sense that shareholder will get the correct share , but it lacks verification protocols to defend against griefing and denial-of-service attacks. Let’s amend the above protocol with some verification steps, inspired by Feldman’s VSS scheme.

Assume for additional safety that the secret-sharing dealer used VSS, and so the public coefficients of are known to all shareholders, such that as in Feldman’s VSS. I’ll also assume that each shareholder can reliably identify who holds which shares, so that a shareholder who does not hold share cannot pose as its bearer.

  1. Once shareholder has sampled coefficients for their partial blinding polynomial , they compute public commitments for those coefficients .



  1. Before evaluating any , shareholder broadcasts their blinding commitment to all other shareholders . In turn, they receive blinding commitments .

Any commitment can be used to compute a public version of the partial blinding polynomial , i.e. to compute on any input .

A shareholder possessing all can compute the public coefficients (those symbols are called theta) of the joint blinding polynomial .


With this, one can compute on any input .

It’s important that every is broadcast over some consistent medium to all other shareholders in in such a way that everyone can be sure they hold the same commitments. If such a broadcast medium isn’t available, shareholders must verify with one-another that they all received the same for every . If someone sent around inconsistent commitments, it would cause the whole issuance process to fail later.

  1. Once all* other shareholders’ commitments are in hand and are universally agreed upon, only then does shareholder compute for all and send each evaluation to shareholder .

* For better efficiency, it is okay for shareholder to optimistically send out blinding polynomial evaluations before receiving all commitments, as long as she only sends out a maximum of evaluations. The last evaluation should only be transmitted once she has all . This section of the security proof explains why.

  1. Upon receiving the partial blinding polynomial evaluation from another shareholder , she verifies that the evaluation matches the commitment .


  1. Shareholders aggregate their partial blinding polynomial evaluations to compute as described in the previous section.

  1. Each shareholder sends to the new inductee shareholder the following data:
  • The public coefficients of the share polynomial : .
  • The public coefficients of blinding polynomial :
  • The new share index .
  • The evaluation of the issuance polynomial .
  1. The new shareholder verifies all the things.
  • Ensure that the sets of public coefficients and for the joint polynomials, as well as the new index given by every shareholder in are all consistent. If not, someone might be trying to play funny games.
  • (optional) If a-priori knowledge of the public point is available or verifiable, now would be a good time to check that it matches .
  • Verify each evaluation is authentic for the given commitments and .

If these checks pass, the new shareholder is confident that yielding their share of the secret polynomial . Remember the whole point of this was to give shareholder a share that would let them help to recover , and hence the secret , which is the constant coefficient of .

  1. Once the new shareholder has valid evaluations of , they can use the points to perform polynomial interpolation to recover the full degree polynomial .



Security Proof

I’m now going to take a stab at proving the security of this protocol. Of course, all this assumes the discrete logarithm problem is hard, and cannot simply compute .

Consider a situation in which a dishonest cabal of malicious shareholders , which is some subset of , attempts to learn some information from the share issuance process which they could use to deduce more information about or the secret . The issuance protocol is secure if learns nothing which they did not already know about or before participating in an execution of the issuance protocol.

Shamir’s Secret Sharing is perfectly secure against malicious shareholders, so as long as consists of fewer than shareholders, they do not yet know any information about before executing the share issuance protocol.

Honest Inductee

Consider when is one share short of a full takeover. Here, is composed of existing malicious shareholders in . The new shareholder and at least one shareholder remain honest.

The only new information which learns during the issuance process is the partial blinding polynomial evaluations , which are sent by the bearer of share to each malicious shareholder in the cabal . This allows to collectively interpolate any using those evaluations, plus the implicit point .

But this is of no use to , because will be totally random if shareholder is honest, and is thus unrelated to or . This gives no additional information.

Since the new shareholder is honest, does not learn or any evaluations thereof.

Malicious Inductee

Consider an alternative situation in which the new shareholder is colluding with , where is now composed of shareholders in . There remain two honest shareholders . This case is more subtle, so let’s take stock of every piece of information that learns in the process, and the relationships between what does not learn.

First, receives the evaluations of the partial blinding polynomials and for all , which are random. does not receive evaluations . To learn these, would need to interpolate the partial blinding polynomials and . This would require learning at least evaluations of each polynomial to supplement the presumed point . As stated, receives only evaluations of each: , and .

does learn the blinding polynomial evaluations on the indexes . This allows them to define relationships between the four unknowns using Lagrange interpolation polynomials. I’ll emphasize the values which does not know.



and are Lagrange Coefficients, defined to interpolate the evaluations of and which are availalbe to .

also learns the two issuance polynomial evaluations, since they are sent to the new and malicious shareholder .


Let’s extract the values which are unknown to from the summation notation, for better readability.


Using these evaluations, can learn the new share , which is related to the shares through a Lagrange interpolation polynomial.


is a set of Lagrange coefficients defined to interpolate each share index in .

Grouping once more to see values known to and those unknown to :

In summary, now has a system of five equations:





…with six unknowns:

This is an undetermined system of equations: It has infinite solutions (technically not infinite solutions, since we’re working in the finite field , but any solution is equally likely). If could learn any one of those unknowns, they would be able to solve the system of equations and unravel the secret-sharing scheme, but as long as at least two shareholders in are honest and keep those values secret, it will be impossible for a malicious subgroup to solve for any secrets.

Trickery

Can fool honest shareholders or into revealing one of these hidden values?

Aside from verification commitments, the only inputs which either honest shareholder accepts from that are used in secret computations are the evaluations of the partial blinding polynomials.

These potentially malicious inputs are summed with honest partial blinding evaluations from the two honest shareholders to compute the evaluations and .


Since all shareholders in are acting in concert, and since all evaluations will be aggregated anyway, let’s simplify and define the evil inputs and such that


will be given and by the honest shareholders. can attempt to choose some evil values of and which reveal information about the unknowns, but this is not possible as and are honestly random. No matter what value of or is chosen by , both evaluations and given to will appear to be randomly chosen.

Rogue Blinding Evaluations

The blinding polynomial commitments are an essential part of this scheme, at least in cases where we’re considering an actively colluding set of shareholders. Commitments must all be received before a shareholder transmits all of his partial blinding polynomial evaluations.

Under certain conditions, a malicious cabal of shareholders can execute a griefing attack, influencing the issuance polynomial evaluation of the one honest shareholder to make him expose his share to the new shareholder . Although shareholder is not part of by definition and so learns nothing from this attack, this would still hurt the honest shareholder and compromise the security of the scheme.

Shareholder will evaluate the issuance polynomial as

If verifiable commitments are not used, or if shareholder doesn’t wait for all blinding polynomial commitments before sending to shareholders , then could wait until they receive all blinding polynomial evaluations from shareholder . They can then interpolate and collectively compute a rogue set of evaluations which they would submit to shareholder .

This fools shareholder into computing which would expose the honest shareholder’s share to the new shareholder .

The new shareholder who receives this evaluation might use to passively observe that . Shareholder has found herself in possession of a duplicate share instead of the new share she intended to learn, .

cannot fully control the output of because they do not know . They could not, for example, cause the new share to evaluate to a number they already know. Even if they could, shareholder would catch such shenanigans when they verify the evaluations .

Note that for efficiency reasons, it would be entirely safe for shareholder to prematurely transmit evaluations of , but hold back the last evaluation in reserve until he receives all . This is because needs at least evaluations of to interpolate it and compute a rogue value of . The cabal already knows one implicit evaluation, . Knowing an additional evaluations of does not give enough information to interpolate , and so they cannot compute .

Security Intuition

Recall we defined as the sum of . The blinding polynomial acts as a shield, jointly built by every shareholder in . This prevents the issuance polynomial from leaking information about the underlying secret polynomial to the new shareholder who recovers it, except for the specific prearranged index at which .

Thanks to , the coefficients of are all a mix of the secret coefficients chosen by the dealer, and the random coefficients sampled uniformly by every shareholder .

Notice that as long as at least one participant sampled her coefficients honestly, then the joint blinding polynomial will also have totally unpredictable coefficients.

Unfortunately for the malicious inductee, every coefficient in is thus scrambled by some random offset. The inductee cannot distinguish between coefficients of given by a real issuance session, and a random set of coefficients, except that they can use to verify .

Otherwise, the malicious inductee could have generated the coefficients of randomly on their own and they would end up with the same distribution of coefficients.

Degrees of Freedom

It is important that the blinding polynomial has degree , and is configured so that every one of its coefficients appears randomly sampled.

If had degree or higher then so would . The new shareholder would need to be given at least evaluations of to interpolate their new share , which is impossible if only shares are available. This breaks usability of the protocol.

On the other hand, also can’t be a polynomial of degree or less without compromising security. If the degree of was or lower, a cabal of shareholders in could interpolate given evaluations of the partial blinding polynomials from the 2 honest shareholders, plus the implicit point .

If the new shareholder also colludes for a total of dishonest parties, then the cabal can compute and find the secret . This breaks our security model, so must have at exactly degree .

Blinding Polynomial Secrecy

It is crucial that the full blinding polynomial must not be learned, especially by the new shareholder . Shareholders should discard their partial blinding polynomial as soon as it is no longer needed. The blinding polynomials must be completely randomly generated, not derived through any deterministic mechanism.

If can be discovered, predicted, or derived by the new shareholder, then the new shareholder can compute to recover the original secret polynomial, and learn the secret .

The joint blinding polynomial coefficients must not be reused for multiple issuance sessions. If the same joint blinding coefficients are used to construct two different issuance polynomials, and , at distinct indexes and respectively, then the two shareholders who interpolated and could collude to recover .

Here's how.

If two distinct issuance polynomials and use the same blinding coefficients, two colluding shareholders can solve a system of equations to compute .

Let represent the jointly chosen random coefficients of , such that



For brevity, let’s define as the reused part of the blinding polynomial.



Phrase in terms of .

This will work out similarly for the alternate issuance polynomial.

Set both sides equal.

Together the colluding shareholders know and , as well as and , so they can solve for .

Index Verification

The shareholders in must ensure that all are distinct from one another and from . Duplicate share indexes would cause divide-by-zero errors when interpolating and possibly lead to unexpected vulnerabilities.

It is also important that each shareholder can positively identify which agents holds which shares when communicating. Agents who misrepresent their share indexes could fool honest shareholders into computing erroneous data.

For example, if a potential new shareholder asks to be issued a share at index , shareholders must not allow this. Jointly computing could result in computing if working in the field of integers (if ), because .

Shareholders who hold multiple shares may equivocate by reporting different share indexes to different peers during the setup phase. If shareholder also controls share legitimately, they could tell other shareholders that they are using either index and give their peers different views of . Both peers could verify and are legitimate indexes for this shareholder, despite the inconsistency. Shareholders should thus also verify that all parties agree on the set of indexes involved in the share recovery procedure. This is left as an exercise to the implementation.

Use Cases

Recovery

Share recovery is probably the most realistic use case for this algorithm. If shareholders maintain a record of who has which share, then they can safely recover lost shares. Records of share ownership are crucial here, so that a phony recovery attempt does not give a malicious shareholder access to new shares they shouldn’t have. For example, Bob might have share , and claims he forgot his share. He might report his share index as instead in an attempt to learn someone else’s share (or learn a completely new share). The other shareholders must be able to verify if is his original share index, to tell if Bob is misbehaving.

As an example, say an employee’s laptop is wiped with a Shamir share share on it. The other staff on their team who - assuming they have at least shares between them - could interactively assist the employee in recovering the lost share without exposing any shares to anyone who shouldn’t have them. This is safe only if the other staff can verify which share the victim had before it was lost.

Users of SLIP39 might find this procedure interesting, as it would allow a user to recover lost SLIP39 shares without having to physically bring the shares together. Yet, I doubt the security of this concept in practice, given the highly sensitive nature of a Bitcoin hardware wallet. To perform interactive share recovery with multi-party computations, the threshold of shares would need to be plugged into separate internet-connected computers, which defeats the purpose of a hardware wallet in the first place.

Interactive share recovery (and all the verification steps) would need to be implemented in hardware wallet firmware, and then all shareholders would need to have a compatible hardware wallet. This is probably much more effort than it is worth. Instead, a user could merely bring a set of shares physically together and reconstitute the full polynomial on the hardware wallet.

Repairable Multisignature

In the case of multisignature, the share recovery protocol would allow signers in polynomial-based threshold signing systems like FROST to recover the long-lived signing shares of signers who experienced some hardware fault or forgot the encryption password for their signing key.

They could also enroll new signers into their group, provided they can mitigate the risk that a new signer might actually be an old signer in a fake mustache.

Repairable Escrow

One could create a redundant 2-of-3 multisignature escrow service in which the user acts as the dealer of shares of a threshold private key. One share (the escrow share) is given to the escrow agent, and two are given to the user. The user can store one of their shares (the cold share) on paper or a USB drive, somewhere safe and offline. The other share (the hot share) can be an online, active-use signing key, used to collaborate with the escrow agent to sign certificates, Bitcoin transactions, emails, etc.

  • The escrow agent acts as a remote second factor, verifying the user with some secondary authentication method like a hardware token, or biometrics.
  • If the user loses one of their shares but retains the other share, the escrow agent can collaborate with the user to recover the lost share trustlessly, thereby returning the user to his original fully functioning state. Other threshold multisignature schemes would require a key migration to fully recover both of the user’s shares.
  • If the escrow agent disappears, the user can independently recover their share with the hot and cold shares, and give the recovered escrow share to a new escrow agent. Colluding escrow agents would be powerless, because they each have the same share.

Alternative Approaches

Sampling Evaluations

One could also design the partial blinding polynomials by sampling random evaluations in instead of sampling random coefficients.

A shareholder would sample random evaluations , one for each index in except for their own.

They would append the fixed point for a total of points, and interpolate the resulting degree polynomial .

The evaluations would be sent to all other shareholders . Shareholder would receive all , and then compute as normal from there, computing on her own.

This alternative approach is a helpful demonstration that however may be constructed, one evaluation of is not truly random, but a function of the other random evaluations, plus the assumed evaluation . At first this seems concerning, but as described above, a colluding subgroup would need at least shareholders who know to interpolate the full polynomial, and shareholder (who receives ) must also participate to make use of this knowledge to learn .

NSG Enrollment

This paper by Stinson and Wei describes a similar approach to issue or recover Shamir shares, in section 2. Unfortunately I only read about this method once I had already finished the majority of this article.

Both methods are very similar and share similar security proofs. Stinson and Wei’s approach might be slightly more efficient in terms of computations, but they also did not describe a verification process to avoid denial-of-service and griefing attacks.

Conclusion

Other interesting extensions to Shamir’s Secret Sharing include changing the threshold, removing a shareholder, or modifying the shared secret in a verifiable fashion.

I might spend a bit of time to write a demo implementation of this algorithm in Python or Rust in the near future if there is sufficient interest.

I have seen some recent interest on the concept of hardware-backed FROST signing tools. Having the ability to recover such a device without the need to migrate keys would be a huge win.

Sources